Bài 10 * trang 172 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho tam giác ABC vuông tại A (AB < AC). Gọi M là trung điểm của BC. Tên tia đối của tia MA lấy điểm D sao cho MD = MA. Trên tia đối của tia CD lấy điểm E sao cho CE = CA.

a) Chứng minh rằng tam giác ACE vuông cân.

b) Kẻ AH vuông góc với BC. Đường thẳng kẻ từ E song song với AC cắt đường thẳng AH tại F. Chứng minh rằng AF = BC.

Lời giải chi tiết

 

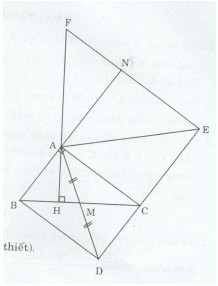
a)Xét tam giác AMC và DMB ta có:

AM = DM (giả thiết)

\(\widehat {AMC} = \widehat {DMB}\)   (hai góc đối đỉnh)

MC = MB (M là trung điểm của BC)

Do đó: \(\eqalign{  & \Delta AMC = \Delta DMB(c.g.c)  \cr  &  \Rightarrow \widehat {ACM} = \widehat {MBD} \cr} \)

Mà hai góc ACM và MBD so le trong nên AC // BD.

Ta có: \(BA \bot AC(\Delta ABC\)  vuông tại A)

AC // BD (chứng minh trên)

\(\Rightarrow CD \bot AC\)

Vậy tam giác ACE vuông tại C.

Ta có: tam giác ACE vuông tại C có: CA = CE (giả thiết)

Do đó: tam giác ACE vuông cân tại C.

b) Gọi N là giao điểm của AB và EF.

Ta có: EF // AC (gt), \(AB \bot AC(\widehat {BAC} = {90^0}) \Rightarrow AB \bot EF\)

Xét tam giác NAE vuông tại N và tam giác CEA vuông tại C có:

AE là cạnh chung.

\(\widehat {AEN} = \widehat {EAC}\)   (so le trong và EF // AC)

Do đó: \(\Delta NAE = \Delta CEA\)  (cạnh huyền - góc nhọn) => AN = CE.

Ta có: AN = CA (= CE).

Xét tam giác NFA và ABC có:

\(\widehat {FNA} = \widehat {BAC}( = {90^0})\)

AN = CA

\(\widehat {NAF} = \widehat {ACB}\)   (cùng phụ với góc HAC)

Do đó: \(\Delta NFA = \Delta ABC(g.c.g)\)  . Vậy AF = BC.