-
Toán 11 tập 1
-
Giải Toán 11 tập 2
Bài 6.12 trang 19 SGK Toán 11 tập 2 - Cùng khám phá
Đề bài
Cho a, b, c là các số thực dương và khác 1. So sánh a, b, c và 1 trong mỗi trường hợp sau:
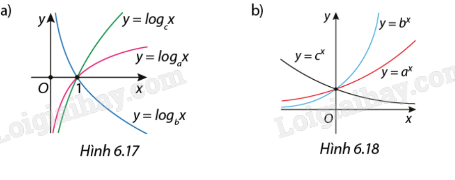
Phương pháp giải - Xem chi tiết
a) Hàm số \(y = {\log _a}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) khi a > 1 và nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) khi 0 < a < 1.
b) Hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) khi a > 1 và nghịch biến trên \(\mathbb{R}\) khi 0 < a < 1.
Lời giải chi tiết
a) Ta thấy hàm số \(y = {\log _a}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) nên a > 1
Ta thấy hàm số \(y = {\log _b}x\) nghịch biến trên khoảng \(\left( {0; + \infty } \right)\) 0 < b < 1
Ta thấy hàm số \(y = {\log _c}x\) đồng biến trên khoảng \(\left( {0; + \infty } \right)\) c > 1
b) Ta thấy hàm số \(y = {a^x}\) đồng biến trên \(\mathbb{R}\) nên a > 1
Ta thấy hàm số \(y = {b^x}\) đồng biến trên \(\mathbb{R}\) nên b > 1
Ta thấy hàm số \(y = {c^x}\) nghịch biến trên \(\mathbb{R}\) nên 0 < c < 1