Bài tập 3 trang 115 Tài liệu dạy – học Toán 7 tập 1

Đề bài

Cho hai đường thẳng cắt nhau, trong bốn góc tạo thành có một góc có số đo bằng 50^o.

a) Hãy kể tên các cặp góc đối đỉnh.

b) Tính số đo của ba góc còn lại.

Lời giải chi tiết

 

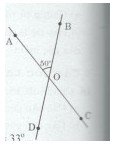
a)\(\widehat {AOB}\)  và \(\widehat {DOC}\)  là hai góc đối đỉnh.

\(\widehat {AOD}\)  và \(\widehat {BOC}\)  là hai góc đối đỉnh.

b) Giả sử \(\widehat {AOB} = {50^0}\)

Cần tính số đo các góc AOD, DOC, BOC.

Hai góc AOB và AOD là hai góc kề bù.

\( \Rightarrow \widehat {AOB} + \widehat {AOD} = {180^0}\)

Do đó: \(\widehat {AOD} = {180^0} - {50^0} = {130^0}\)

Ta có: \(\widehat {DOC} = \widehat {AOB}\)  (hai góc đối đỉnh) nên \(\widehat {DOC} = {50^0}\)

Mặt khác \(\widehat {BOC} = \widehat {AOD}\)  (hai góc đối đỉnh) nên \(\widehat {BOC} = {130^0}\)