Câu 15 trang 102 SGK Hình học 11 Nâng cao

Đề bài

Cho tứ diện ABCD. Tìm điểm O cách đều bốn đỉnh của tứ diện.

Lời giải chi tiết

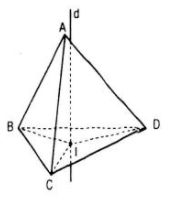
Gọi I là tâm đường tròn ngoại tiếp của ΔBCD

Gọi d là đường thẳng đi qua I và vuông góc với mặt phẳng (BCD)

Theo kết quả bài 14. M ϵ d ⇔ MB = MC = MD

(d gọi là trục của đường tròn ngoại tiếp tam giác BCD)

Gọi O là giao điểm của d với mặt phẳng trung trực của AB.

=> OA = OB ( vì O thuộc mặt phẳng trung trực của AB).

Và OB = OC = OD ( vì O thuộc đường thẳng d).

Suy ra :OA = OB = OC = OD hay O cách đều bốn đỉnh của tứ diện (O gọi là tâm mặt cầu ngoại tiếp tứ diện ABCD).