- Trang chủ
- Lớp 11
- Toán học Lớp 11
- SGK Toán 11 Nâng cao Lớp 11
- HÌNH HỌC- TOÁN 11 NÂNG CAO
- CHƯƠNG III: VECTƠ TRONG KHÔNG GIAN. QUAN HỆ VUÔNG GÓC
-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO

-
HÌNH HỌC- TOÁN 11 NÂNG CAO

Câu 27 trang 112 SGK Hình học 11 Nâng cao
Đề bài
Cho hai tam giác ACD, BCD nằm trên hai mặt phẳng vuông góc với nhau và AC = AD = BC = BD = a, CD = 2x. Gọi I, J lần lượt là trung điểm của AB và CD.
a. Tính AB, IJ theo a và x.
b. Với giá trị nào của x thì hai mặt phẳng (ABC) và (ABD) vuông góc ?
Lời giải chi tiết
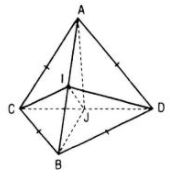
a. Vì J là trung điểm của CD và AC = AD nên AJ ⊥ CD.
Do mp(ACD) ⊥ mp(BCD) nên AJ ⊥ mp(BCD)
Mặt khác, AC = AD = BC = BD nên tam giác AJB vuông cân, suy ra \(AB = AJ\sqrt 2 ,A{J^2} = {a^2} - {x^2}\) \(hay\,AJ = \sqrt {{a^2} - {x^2}} .\)
Vậy \(AB = \sqrt {2\left( {{a^2} - {x^2}} \right)} \) với a > x
Do IA = IB, tam giác AJB vuông tại J nên \(JI = {1 \over 2}AB,\) tức là \(IJ = {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)} .\)
b)
+Tam giác ABC có AC = BC
nên tam giác ABC cân tại C,
có CI là đường trung tuyến nên đồng thời là đường cao:
CI ⊥ AB (3)
Tam giác ABD cân tại D có DI là đường trung tuyến nên
DI ⊥ AB (4)
Hai mp (ABC) và (ABD) cắt nhau theo giao tuyến là AB (5)
Từ (3) , (4) và (5) suy ra góc giữa hai mp(ABC) và (ABD) là góc CID.
Vậy mp(ABC) ⊥ mp(ABD) \( \Leftrightarrow \widehat {CID} = 90^\circ \)
\( \Leftrightarrow IJ = {1 \over 2}CD\) \(\Leftrightarrow {1 \over 2}\sqrt {2\left( {{a^2} - {x^2}} \right)} = {1 \over 2}.2x\) \(\Leftrightarrow 2\left( {{a^2} - {x^2}} \right) = 4{x^2} \Leftrightarrow {a^2} = 3{x^2}\)
\(\Leftrightarrow x = {{a\sqrt 3 } \over 3}\)
