- Trang chủ
- Lớp 11
- Toán học Lớp 11
- SGK Toán 11 Nâng cao Lớp 11
- HÌNH HỌC- TOÁN 11 NÂNG CAO
- CHƯƠNG II: ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN. QUAN HỆ SONG SONG
-
ĐẠI SỐ VÀ GIẢI TÍCH - TOÁN 11 NÂNG CAO

-
HÌNH HỌC- TOÁN 11 NÂNG CAO

Câu 9 trang 50 SGK Hình học 11 Nâng cao
Đề bài
Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng sao cho chúng đôi một cắt nhau. Chứng minh rằng chúng đồng quy
Lời giải chi tiết
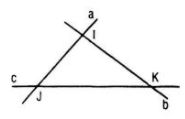
Gọi \(I =a\cap b\) \( \Rightarrow \left\{ \begin{array}{l}
I \in {a}\\
I \in {b}
\end{array} \right.\)
Ta chứng minh \(I ∈ c\). Thật vậy,
Gọi (β) là mặt phẳng chứa hai đường thẳng cắt nhau \(a,c\).
\((\gamma)\) là mặt phẳng chứa hai đường thẳng cắt nhau \(b,c\).
Do ba đường thẳng không cùng nằm trong một mặt phẳng nên (β) và \((\gamma)\) phân biệt.
Ngoài ra
\(\left\{ \begin{array}{l}
{c} \subset \left( \beta \right)\\
{c} \subset \left( \gamma \right)
\end{array} \right. \Rightarrow \left( \beta \right) \cap \left( \gamma \right) = {c}\)
\(I ∈ a\subset \left( \beta \right) \Rightarrow I ∈ (β) = (a,c)\)
\(I ∈ b\subset \left( \gamma \right) \Rightarrow I ∈ (\gamma) = (b,c)\)
Từ đó suy ra, \(I ∈(\beta ) \cap (\gamma )=c\).
Cách khác:
Gọi \(\left( P \right)\) là mặt phẳng chứa hai đường thẳng cắt nhau \(b\) và \(c\).
Gọi
\(\begin{array}{l}I = a \cap b \Rightarrow I \in b \subset \left( P \right)\\J = a \cap c \Rightarrow J \in c \subset \left( P \right)\end{array}\)
Nếu \(I,J\) phân biệt thì \(a\) đi qua cả \(I\) và \(J\) hay \(a \equiv IJ \subset \left( P \right)\)
Do đó \(a,b,c\) cùng nằm trong \(\left( P \right)\) (mâu thuẫn)
Do đó \(I \equiv J\) là điểm thuộc cả \(a,b,c\).
Vậy \(a,b,c\) đồng qui.
