-
Đề thi giữa kì 1
-
1. Đề thi giữa kì 1 - Đề số 1
-
2. Đề thi giữa kì 1 - Đề số 2
-
3. Đề thi giữa kì 1 - Đề số 3
-
4. Đề thi giữa kì 1 - Đề số 4
-
5. Đề thi giữa kì 1 - Đề số 5
-
6. Đề thi giữa kì 1 - Đề số 6
-
7. Đề thi giữa kì 1 - Đề số 7
-
8. Đề thi giữa kì 1 - Đề số 8
-
9. Đề thi giữa kì 1 - Đề số 9
-
10. Đề thi giữa kì 1 - Đề số 10
-
11. Đề thi giữa kì 1 - Đề số 11
-
12. Đề thi giữa kì 1 - Đề số 12
-
13. Đề thi giữa kì 1 - Đề số 13
-
14. Đề thi giữa kì 1 - Đề số 14
-
15. Đề thi giữa kì 1 - Đề số 15
-
16. Đề thi giữa kì 1 - Đề số 16
-
17. Đề thi giữa kì 1 - Đề số 17
-
18. Đề thi giữa kì 1 - Đề số 18
-
-
Đề thi học kì 1
-
1. Đề cương ôn tập học kì 1
-
2. Đề thi học kì 1 - Đề số 1
-
3. Đề thi học kì 1 - Đề số 2
-
4. Đề thi học kì 1 - Đề số 3
-
5. Đề thi học kì 1 - Đề số 4
-
6. Đề thi học kì 1 - Đề số 5
-
7. Đề thi học kì 1 - Đề số 6
-
8. Đề thi học kì 1 - Đề số 7
-
9. Đề thi học kì 1 - Đề số 8
-
10. Đề thi học kì 1 - Đề số 9
-
11. Đề thi học kì 1 - Đề số 10
-
12. Đề thi học kì 1 - Đề số 11
-
13. Đề thi học kì 1 - Đề số 12
-
14. Đề thi học kì 1 - Đề số 13
-
15. Đề thi học kì 1 - Đề số 14
-
16. Đề thi học kì 1 - Đề số 15
-
-
Đề thi giữa kì 2
-
1. Đề thi giữa kì 2 - Đề số 1
-
2. Đề thi giữa kì 2 - Đề số 2
-
3. Đề thi giữa kì 2 - Đề số 3
-
4. Đề thi giữa kì 2 - Đề số 4
-
5. Đề thi giữa kì 2 - Đề số 5
-
6. Đề thi giữa kì 2 - Đề số 6
-
7. Đề thi giữa kì 2 - Đề số 7
-
8. Đề thi giữa kì 2 - Đề số 8
-
9. Đề thi giữa kì 2 - Đề số 9
-
10. Đề thi giữa kì 2 - Đề số 10
-
-
Đề thi học kì 2
-
1. Đề cương ôn tập học kì 2
-
2. Đề thi học kì 2 - Đề số 1
-
3. Đề thi học kì 2 - Đề số 2
-
4. Đề thi học kì 2 - Đề số 3
-
5. Đề thi học kì 2 - Đề số 4
-
6. Đề thi học kì 2 - Đề số 5
-
7. Đề thi học kì 2 - Đề số 6
-
8. Đề thi học kì 2 - Đề số 7
-
9. Đề thi học kì 2 - Đề số 8
-
10. Đề thi học kì 2 - Đề số 9
-
11. Đề thi học kì 2 - Đề số 10
-
12. Đề thi học kì 2 - Đề số 11
-
13. Đề thi học kì 2 - Đề số 12
-
14. Đề thi học kì 2 - Đề số 13
-
Đề thi giữa kì 2 Toán 6 Chân trời sáng tạo - Đề số 9
Đề bài
Phân số nghịch đảo của phân số \(\frac{1}{3}\) là
- A. \(3\).
- B. \( - \frac{1}{3}\).
- C. \( - 3\).
- D. \(1\).
Khẳng định nào sau đây đúng?
- A. \( - \frac{2}{7} > \frac{1}{7}\).
- B. \(\frac{2}{7} < \frac{1}{7}\).
- C. \(\frac{2}{7} = - \frac{1}{7}\).
- D. \(\frac{2}{7} > \frac{1}{7}\).
Cho \(\frac{3}{4}x = 1\frac{2}{3}\). Kết quả giá trị x là:
- A. \(\frac{{20}}{9}\).
- B. \(\frac{5}{4}\).
- C. \(\frac{{29}}{{12}}\).
- D. \(\frac{{11}}{{12}}\).
Cho a, b, m là các số nguyên, m khác 0. Tổng \(\frac{a}{m} + \frac{b}{m}\) bằng
- A. \(\frac{{a + b}}{{m + m}}\).
- B. \(\frac{{a + b}}{{m.m}}\).
- C. \(\frac{{a + b}}{m}\).
- D. \(a + b\).
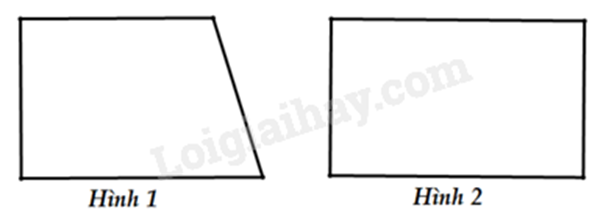
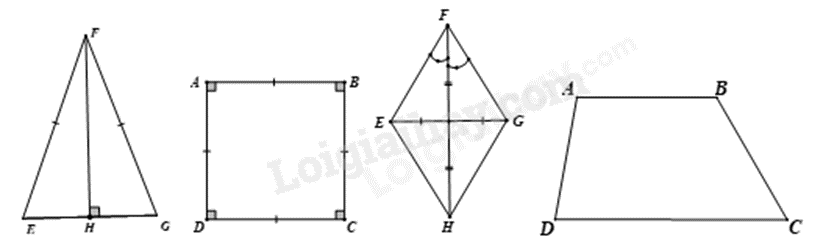
- A. Hình 1.
- B. Hình 2.
- C. Hình 3.
- D. Hình 4.
- A. Chữ có tâm đối xứng là: O.
- B. Chữ có tâm đối xứng là: G.
- C. Chữ có tâm đối xứng là: A.
- D. Chữ có tâm đối xứng là: A; O.
- A. 0.
- B. 1.
- C. 2.
- D. 3.
- A. Điểm đối xứng với A qua đường thẳng d là A.
- B. Điểm đối xứng với A qua đường thẳng d là B.
- C. Điểm đối xứng với B qua đường thẳng d là B.
- D. Điểm đối xứng với Q qua đường thẳng d là Q.
- A. Điểm E và B.
- B. Điểm C và F.
- C. Điểm F và B.
- D. Điểm A, E và C.
- A. Ba điểm A, F, E thẳng hàng.
- B. Ba điểm A, B, C thẳng hàng.
- C. Ba điểm A, E, C thằng hàng.
- D. Ba điểm E, B, C thẳng hàng.
- A. Hình 2.
- B. Hình 3.
- C. Hình 4.
- D. Hình 1.
Cho \(I\) là trung điểm của đoạn thẳng \(AB\). Biết \(AB = 10cm\), số đo của đoạn thẳng \(IB\) là
- A. 4cm.
- B. 5cm.
- C. 6cm.
- D. 20cm.
Thực hiện các phép tính sau (tính hợp lý nếu có thể).
a) \(\frac{{ - 2}}{{11}} + \frac{{ - 9}}{{11}}\)
b) \(\frac{1}{2} - \frac{{ - 3}}{4}\)
c) \(\frac{{12}}{{11}} - \frac{{ - 7}}{{19}} + \frac{{12}}{{19}}\)
d) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\)
Lời giải và đáp án
Phân số nghịch đảo của phân số \(\frac{1}{3}\) là
- A. \(3\).
- B. \( - \frac{1}{3}\).
- C. \( - 3\).
- D. \(1\).
Đáp án : A
Phân số nghịch đảo của phân số \(\frac{a}{b}\) là \(\frac{b}{a}\) \(\left( {\frac{a}{b}.\frac{b}{a} = 1} \right)\)
Phân số nghịch đảo của phân số \(\frac{1}{3}\) là \(3\).
Đáp án A.
Khẳng định nào sau đây đúng?
- A. \( - \frac{2}{7} > \frac{1}{7}\).
- B. \(\frac{2}{7} < \frac{1}{7}\).
- C. \(\frac{2}{7} = - \frac{1}{7}\).
- D. \(\frac{2}{7} > \frac{1}{7}\).
Đáp án : D
So sánh hai phân số cùng mẫu.
Ta có \( - 2 < 1\) nên \(\frac{{ - 2}}{7} < \frac{1}{7}\) (A sai).
\(2 > 1\) nên \(\frac{2}{7} > \frac{1}{7}\) (B sai).
\(2 \ne - 1\) nên \(\frac{2}{7} \ne - \frac{1}{7}\) (C sai)
\(2 > 1\) nên \(\frac{2}{7} > \frac{1}{7}\) (D đúng)
Đáp án D.
Cho \(\frac{3}{4}x = 1\frac{2}{3}\). Kết quả giá trị x là:
- A. \(\frac{{20}}{9}\).
- B. \(\frac{5}{4}\).
- C. \(\frac{{29}}{{12}}\).
- D. \(\frac{{11}}{{12}}\).
Đáp án : A
Sử dụng quy tắc tính với phân số.
\(\begin{array}{l}\frac{3}{4}x = 1\frac{2}{3}\\\frac{3}{4}x = \frac{5}{3}\\x = \frac{5}{3}:\frac{3}{4}\\x = \frac{{20}}{9}\end{array}\)
Đáp án A.
Cho a, b, m là các số nguyên, m khác 0. Tổng \(\frac{a}{m} + \frac{b}{m}\) bằng
- A. \(\frac{{a + b}}{{m + m}}\).
- B. \(\frac{{a + b}}{{m.m}}\).
- C. \(\frac{{a + b}}{m}\).
- D. \(a + b\).
Đáp án : C
Dựa vào quy tắc cộng hai phân số cùng mẫu.
\(\frac{a}{m} + \frac{b}{m} = \frac{{a + b}}{m}\)
Đáp án C.
- A. Hình 1.
- B. Hình 2.
- C. Hình 3.
- D. Hình 4.
Đáp án : A
Dựa vào kiến thức về trục đối xứng.
Hình có trục đối xứng là hình 1.
Đáp án A.
- A. Chữ có tâm đối xứng là: O.
- B. Chữ có tâm đối xứng là: G.
- C. Chữ có tâm đối xứng là: A.
- D. Chữ có tâm đối xứng là: A; O.
Đáp án : B
Dựa vào kiến thức về tâm đối xứng.
Hình có tâm đối xứng là hình O.
Đáp án B.
- A. 0.
- B. 1.
- C. 2.
- D. 3.
Đáp án : C
Dựa vào kiến thức về trục đối xứng.
Có 2 hình có trục đối xứng
Đáp án C.
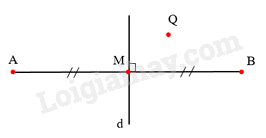
- A. Điểm đối xứng với A qua đường thẳng d là A.
- B. Điểm đối xứng với A qua đường thẳng d là B.
- C. Điểm đối xứng với B qua đường thẳng d là B.
- D. Điểm đối xứng với Q qua đường thẳng d là Q.
Đáp án : B
Dựa vào kiến thức về trục đối xứng.
Điểm đối xứng với A qua đường thẳng d là B nên B đúng.
Đáp án B.
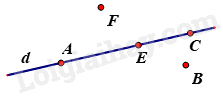
- A. Điểm E và B.
- B. Điểm C và F.
- C. Điểm F và B.
- D. Điểm A, E và C.
Đáp án : D
Quan sát hình vẽ để trả lời.
Điểm thuộc đường thẳng d là A, E, C.
Đáp án D.
- A. Ba điểm A, F, E thẳng hàng.
- B. Ba điểm A, B, C thẳng hàng.
- C. Ba điểm A, E, C thằng hàng.
- D. Ba điểm E, B, C thẳng hàng.
Đáp án : C
Ba điểm cùng thuộc một đường thẳng thì thẳng hàng.
Vì A, E, C nằm trên đường thẳng d nên chúng thẳng hàng.
Đáp án C.
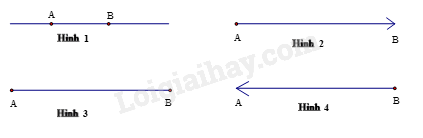
- A. Hình 2.
- B. Hình 3.
- C. Hình 4.
- D. Hình 1.
Đáp án : B
Dựa vào kiến thức về đoạn thẳng.
Hình vẽ đoạn thẳng AB là hình 3.
Đáp án B.
Cho \(I\) là trung điểm của đoạn thẳng \(AB\). Biết \(AB = 10cm\), số đo của đoạn thẳng \(IB\) là
- A. 4cm.
- B. 5cm.
- C. 6cm.
- D. 20cm.
Đáp án : B
Dựa vào kiến thức về trung điểm của đoạn thẳng.
Vì I là trung điểm của AB nên AI = IB = \(\frac{1}{2}\)AB = \(\frac{1}{2}\).10 = 5(cm).
Đáp án B.
Thực hiện các phép tính sau (tính hợp lý nếu có thể).
a) \(\frac{{ - 2}}{{11}} + \frac{{ - 9}}{{11}}\)
b) \(\frac{1}{2} - \frac{{ - 3}}{4}\)
c) \(\frac{{12}}{{11}} - \frac{{ - 7}}{{19}} + \frac{{12}}{{19}}\)
d) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7}\)
Dựa vào quy tắc tính với phân số.
a) \(\frac{{ - 2}}{{11}} + \frac{{ - 9}}{{11}} = \frac{{ - 2 + ( - 9)}}{{11}} = \frac{{ - 11}}{{11}} = - 1\)
b) \(\frac{1}{2} - \frac{{ - 3}}{4} = \frac{{1.2}}{{2.2}} - \frac{{ - 3}}{4} = \frac{2}{4} - \frac{{ - 3}}{4} = \frac{{2 - ( - 3)}}{4} = \frac{5}{4}.\)
c) \(\frac{{12}}{{11}} - \frac{{ - 7}}{{19}} + \frac{{12}}{{19}}\) \( = \frac{{12}}{{11}} + \frac{7}{{19}} + \frac{{12}}{{19}}\) \( = \frac{{12}}{{11}} + \left( {\frac{7}{{19}} + \frac{{12}}{{19}}} \right)\) \( = \frac{{12}}{{11}} + 1\) \( = \frac{{12}}{{11}} + \frac{{11}}{{11}}\) \( = \frac{{23}}{{11}}.\)
d) \(\frac{{ - 5}}{7} \cdot \frac{2}{{11}} + \frac{{ - 5}}{7} \cdot \frac{9}{{11}} + \frac{5}{7} = \frac{{ - 5}}{7}\left( {\frac{2}{{11}} + \frac{9}{{11}}} \right) + \frac{5}{7} = \frac{{ - 5}}{7} \cdot 1 + \frac{5}{7} = 0\)
Dựa vào kiến thức về trục đối xứng, tâm đối xứng.
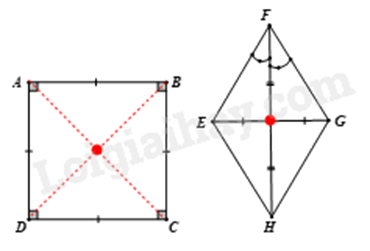
a) Hình có trục đối xứng là hình 2.
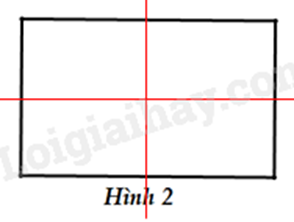
b) Các hình có tâm đối xứng là hình vuông, hình thoi. Tâm đối xứng của hình vuông và hình thoi là giao điểm của hai đường chéo.
Tính số học sinh tốt theo số học sinh cả lớp bằng tổng số học sinh cả lớp . \(\frac{1}{7}\)
Tính số học sinh khá và đạt để suy ra số học sinh khá bằng tổng số học sinh cả lớp – số học sinh tốt.
Số học sinh đạt bằng tổng số học sinh khá và đạt – số học sinh khá.
Số học sinh tốt là: \(42.\frac{1}{7} = 6\)( học sinh)
Số học sinh khá là: \((42 - 6).\frac{2}{3} = 24\)(học sinh)
Số học sinh đạt là : \(42 - 6 - 24 = 12\)(học sinh)
a) So sánh BA với BC để xác định điểm nằm giữa.
b) Chứng minh B nằm giữa O và C và BO = BC nên B là trung điểm của OC.
a) Trên tia Bx ta có BA = 2cm, BC = 3cm vì 2 < 3 nên BA < BC, vậy, A nằm giữa B và C.
Khi đó ta có : BA + AC = BC suy ra \(AC = BC - BA\) suy ra \(AC = 3 - 2 = 1\)
Vậy AC = 1cm.
b) Ta có O thuộc tia đối của tia Bx, nên O và C nằm khác phía đối với B hay B nằm giữa O và C.
Khi đó: OB + BC = OC. (1)
Mà theo đề bài: BO = BC = 3cm (2)
Từ (1) và (2), suy ra B là trung điểm của OC.
Rút gọn A, biến đổi các phân số trong A để rút gọn.
\(\begin{array}{l}S = \left( {1 - \frac{1}{4}} \right).\left( {1 - \frac{1}{9}} \right).\left( {1 - \frac{1}{{16}}} \right).\left( {1 - \frac{1}{{25}}} \right)\left( {1 - \frac{1}{{36}}} \right)...\left( {1 - \frac{1}{{9901}}} \right)\\ = \frac{3}{4} \cdot \frac{8}{9} \cdot \frac{{15}}{{16}} \cdot \frac{{24}}{{25}} \cdot \frac{{35}}{{36}} \cdots \frac{{9800}}{{99}}\\ = \frac{{1.3}}{{2.2}} \cdot \frac{{2.4}}{{3.3}} \cdot \frac{{3.5}}{{4.4}} \cdot \frac{{4.6}}{{5.5}} \cdot \frac{{5.7}}{{6.6}} \cdots \frac{{98.100}}{{99.99}}\\ = \frac{{1.2.3.4.5...98}}{{2.3.4.5.6...99}} \cdot \frac{{3.4.5.6.7...100}}{{2.3.4.5.6...99}}\\ = \frac{1}{{99}} \cdot \frac{{100}}{2}\\ = \frac{{50}}{{99}} \cdot \end{array}\)
Vậy \(S = \frac{{50}}{{99}}\).