Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 10

Đề bài

I. Trắc nghiệm

Câu 1 :

Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:

A.
\(\frac{{30}}{{40}}\)
B.
\(\frac{1}{4}\).
C.
\(\frac{3}{4}\)
D.
\(\frac{6}{8}\)

Câu 2 :

Giá trị \(\frac{3}{4}\) của – 60 là:

A.
80.
B.
- 80.
C.
45.
D.
- 45.

Câu 3 :

Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi

A.
\(a.3 = b.4\).
B.
\(a.4 = 3.b\).
C.
\(a + 4 = b + 3\).
D.
\(a - 4 = b - 3\).

Câu 4 :

Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?

A.
\(\frac{9}{{21}}\).
B.
\(\frac{{ - 3}}{7}\).
C.
\(\frac{3}{7}\).
D.
\(\frac{{ - 9}}{{21}}\).

Câu 5 :

Số đối của số -3,68 là:

A.
368.
B.
3,68.
C.
3,86.
D.
3,86.

Câu 6 :

Kết quả làm tròn số 12,567537 đến chữ số thập phân thứ ba là

A.
12,567.
B.
12,568.
C.
12,600.
D.
12,570.

Câu 7 :

Tính \(14,9 + ( - 8,3) + ( - 4,9)\). Kết quả là:

A.
\(18,3.\)
B.
\( - 18,3.\)
C.
\(1,7.\)
D.
-7.

Câu 8 :

Chiếc túi xách có giá trị 200 000 đồng. Cửa hàng kích cầu tiêu dùng nên giảm giá 15%. Hỏi sau khi giảm chiếc túi xách có giá là bao nhiêu nghìn đồng?

A.
170.
B.
165.
C.
160.
D.
150.

Câu 9 :

Cho hình vẽ sau.

Đường thẳng n đi qua điểm nào?

A.
Điểm A.
B.
Điểm B và điểm C.
C.
Điểm B và điểm D.
D.
Điểm D và điểm C.

Câu 10 :

Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là

A.
tia QF.
B.
tia QP.
C.
tia FP.
D.
tia PF.

Câu 11 :

Em hãy chọn câu đúng.

A.
Qua hai điểm phân biệt có vô số đường thẳng.
B.
Có vô số điểm cùng thuộc một đường thẳng.
C.
Hai đường thẳng phân biệt thì song song.
D.
Trong ba điểm thẳng hàng thì có hai điểm nằm giữa.

Câu 12 :

Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau?

A.
Hai đường thẳng AB và AC cắt nhau.
B.
Hai đường thẳng AB và AC song song với nhau.
C.
Hai đường thẳng AB và AC trùng nhau.
D.
Hai đường thẳng AB và AC có hai điểm chung.

II. Tự luận

Câu 1 :

Thực hiện các phép tính sau (tính hợp lý nếu có thể).

a) \(\frac{{ - 3}}{7} + \frac{5}{7}\)

b) \(\frac{2}{3} + \frac{{ - 3}}{5}\)

c) \(\frac{2}{9} - \left( {\frac{1}{{20}} + \frac{2}{9}} \right)\)

d) \(\frac{{11}}{{23}}.\frac{{12}}{{17}} + \frac{{11}}{{23}}.\frac{5}{{17}} + \frac{{12}}{{23}}\)

Câu 2 :

Tìm \(x\), biết:

a) x + 5,5 = 16,5

b) \(\frac{3}{5}x - \frac{1}{3} = \frac{7}{3}\)

Câu 3 :

Một người bán một số gạo trong 3 ngày. Ngày thứ nhất bán \(\frac{1}{3}\) số gạo. Ngày thứ hai bán \(\frac{4}{9}\) số gạo còn lại. Ngày thứ ba người ấy bán nốt \(1400\,kg\) gạo. Tính số gạo bán trong cả ba ngày?

Câu 4 :

Trên tia Ox lấy hai điểm A và B sao cho OA = 3cm , OB = 6cm.

a) Chứng tỏ rằng: A là trung điểm của OB.

b) Trên tia đối của tia Ox lấy điểm K sao cho OK = So sánh KA và AB.

Câu 5 :

Một cửa hàng pizza có chương trình khuyến mãi như sau, mua 1 cái giảm 30% giá bán, mua từ cái thứ 2 giảm thêm 5% trên giá đã giảm cái bánh thứ 1. Hỏi nếu mua 2 cái bánh, em phải trả tối thiểu bao nhiêu tiền? Biết giá bánh ban đầu là 210.000 đồng một cái (àm tròn đến hàng nghìn đồng)

Lời giải và đáp án

I. Trắc nghiệm

Câu 1 :

Phân số nào dưới đây không biểu diễn phần tô màu cam trong hình bên:

A.
\(\frac{{30}}{{40}}\)
B.
\(\frac{1}{4}\).
C.
\(\frac{3}{4}\)
D.
\(\frac{6}{8}\)

Đáp án : B

Phương pháp giải :

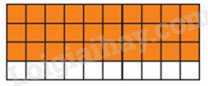
Quan sát hình vẽ và tìm các phân số bằng với phân số đó..

Lời giải chi tiết :

Ta thấy trong hình có 40 ô và có 30 ô màu cam nên ta có phân số biểu diễn phần tô màu cam trong hình bên là \(\frac{{30}}{{40}}\).

Các phân số bằng với phân số \(\frac{{30}}{{40}}\) là \(\frac{3}{4}\) và \(\frac{6}{8}\).

Vậy phân số không biểu diễn là phân số \(\frac{1}{4}\).

Đáp án B.

Câu 2 :

Giá trị \(\frac{3}{4}\) của – 60 là:

A.
80.
B.
- 80.
C.
45.
D.
- 45.

Đáp án : D

Phương pháp giải :

Tính \(\frac{m}{n}\) của a bằng \(a.\frac{m}{n}\).

Lời giải chi tiết :

Giá trị \(\frac{3}{4}\) của – 60 là: \(\left( { - 60} \right).\frac{3}{4} = - 45\).

Đáp án D.

Câu 3 :

Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi

A.
\(a.3 = b.4\).
B.
\(a.4 = 3.b\).
C.
\(a + 4 = b + 3\).
D.
\(a - 4 = b - 3\).

Đáp án : B

Phương pháp giải :

Hai phân số \(\frac{a}{b} = \frac{c}{d}\) khi \(ad = bc\).

Lời giải chi tiết :

Hai phân số \(\frac{a}{b} = \frac{3}{4}\) khi \(a.4 = 3.b\).

Đáp án B.

Câu 4 :

Khi rút gọn phân \(\frac{{ - 27}}{{63}}\) ta được phân số tối giản là số nào sau đây?

A.
\(\frac{9}{{21}}\).
B.
\(\frac{{ - 3}}{7}\).
C.
\(\frac{3}{7}\).
D.
\(\frac{{ - 9}}{{21}}\).

Đáp án : B

Phương pháp giải :

Sử dụng quy tắc rút gọn phân số.

Lời giải chi tiết :

\(\frac{{ - 27}}{{63}} = \frac{{ - 27:9}}{{63:9}} = \frac{{ - 3}}{7}\).

Đáp án B.

Câu 5 :

Số đối của số -3,68 là:

A.
368.
B.
3,68.
C.
3,86.
D.
3,86.

Đáp án : B

Phương pháp giải :

Số đối của a là – a.

Lời giải chi tiết :

Số đối của số -3,68 là 3,68.

Đáp án B.

Câu 6 :

Kết quả làm tròn số 12,567537 đến chữ số thập phân thứ ba là

A.
12,567.
B.
12,568.
C.
12,600.
D.
12,570.

Đáp án : B

Phương pháp giải :

Dựa vào quy tắc làm tròn số.

Lời giải chi tiết :

Số 12,567537 làm tròn đến chữ số thập phân thứ ba là 12,568.

Đáp án B.

Câu 7 :

Tính \(14,9 + ( - 8,3) + ( - 4,9)\). Kết quả là:

A.
\(18,3.\)
B.
\( - 18,3.\)
C.
\(1,7.\)
D.
-7.

Đáp án : C

Phương pháp giải :

Nhóm nhân tử để tính nhanh.

Lời giải chi tiết :

\(\begin{array}{l}14,9 + ( - 8,3) + ( - 4,9)\\ = \left( {14,9 - 4,9} \right) - 8.3\\ = 10 - 8,3\\ = 1,7\end{array}\)

Đáp án C.

Câu 8 :

Chiếc túi xách có giá trị 200 000 đồng. Cửa hàng kích cầu tiêu dùng nên giảm giá 15%. Hỏi sau khi giảm chiếc túi xách có giá là bao nhiêu nghìn đồng?

A.
170.
B.
165.
C.
160.
D.
150.

Đáp án : A

Phương pháp giải :

Tính \(m\% \) của a bằng \(a.m\% = a.\frac{m}{{100}}\).

Lời giải chi tiết :

Chiếc túi xách được giảm số tiền là:

\(200.15\% = \,200.\frac{{15}}{{100}} = 30\) (nghìn đồng)

Vậy sau khi giảm, chiếc túi sách có giá là:

200 – 30 = 170 (nghìn đồng).

Đáp án A.

Câu 9 :

Cho hình vẽ sau.

Đường thẳng n đi qua điểm nào?

A.
Điểm A.
B.
Điểm B và điểm C.
C.
Điểm B và điểm D.
D.
Điểm D và điểm C.

Đáp án : B

Phương pháp giải :

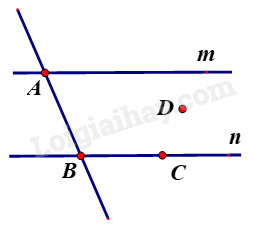
Quan sát hình vẽ để trả lời.

Lời giải chi tiết :

Đường thẳng n đi qua điểm B và điểm C

Đáp án B.

Câu 10 :

Cho F là điểm nằm giữa hai điểm P và Q. Khi đó tia đối của tia FQ là

A.
tia QF.
B.
tia QP.
C.
tia FP.
D.
tia PF.

Đáp án : C

Phương pháp giải :

Dựa vào kiến thức về tia đối.

Lời giải chi tiết :

Tia đối của tia FQ là tia FP (vì F nằm giữa P và Q).

Đáp án C.

Câu 11 :

Em hãy chọn câu đúng.

A.
Qua hai điểm phân biệt có vô số đường thẳng.
B.
Có vô số điểm cùng thuộc một đường thẳng.
C.
Hai đường thẳng phân biệt thì song song.
D.
Trong ba điểm thẳng hàng thì có hai điểm nằm giữa.

Đáp án : B

Phương pháp giải :

Dựa vào kiến thức về đường thẳng.

Lời giải chi tiết :

Qua hai điểm phân biệt chỉ có 1 đường thẳng nên A sai.

Có vô số điểm cùng thuộc một đường thẳng. nên B đúng.

Hai đường thẳng phân biết chưa chắc đã song song nên C sai.

Trong ba điểm thẳng hàng chỉ có một điểm nằm giữa nên D sai.

Đáp án B.

Câu 12 :

Dựa vào hình vẽ, hãy chọn khẳng định đúng trong các khẳng định sau?

A.
Hai đường thẳng AB và AC cắt nhau.
B.
Hai đường thẳng AB và AC song song với nhau.
C.
Hai đường thẳng AB và AC trùng nhau.
D.
Hai đường thẳng AB và AC có hai điểm chung.

Đáp án : A

Phương pháp giải :

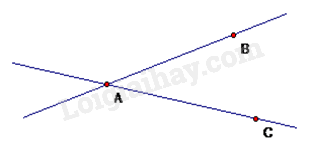
Quan sát hình vẽ để xác định.

Lời giải chi tiết :

Hai đường thẳng AB và AC cắt nhau tại A.

Đáp án A.

II. Tự luận

Câu 1 :

Thực hiện các phép tính sau (tính hợp lý nếu có thể).

a) \(\frac{{ - 3}}{7} + \frac{5}{7}\)

b) \(\frac{2}{3} + \frac{{ - 3}}{5}\)

c) \(\frac{2}{9} - \left( {\frac{1}{{20}} + \frac{2}{9}} \right)\)

d) \(\frac{{11}}{{23}}.\frac{{12}}{{17}} + \frac{{11}}{{23}}.\frac{5}{{17}} + \frac{{12}}{{23}}\)

Phương pháp giải :

Dựa vào quy tắc tính với phân số.

Lời giải chi tiết :

a) \(\frac{{ - 3}}{7} + \frac{5}{7} = \frac{2}{7}\)

b) \(\frac{2}{3} + \frac{{ - 3}}{5} = \frac{{10}}{{15}} + \frac{{ - 9}}{{15}} = \frac{1}{{15}}\)

c) \(\frac{2}{9} - \left( {\frac{1}{{20}} + \frac{2}{9}} \right) = \frac{2}{9} - \frac{1}{{20}} - \frac{2}{9} = - \frac{1}{{20}}\)

d) \(\frac{{11}}{{23}}.\frac{{12}}{{17}} + \frac{{11}}{{23}}.\frac{5}{{17}} + \frac{{12}}{{23}}\)\( = \frac{{11}}{{23}}.\left( {\frac{{12}}{{17}} + \frac{5}{{17}}} \right) + \frac{{12}}{{23}}\) \( = \frac{{11}}{{23}} \cdot 1 + \frac{{12}}{{23}}\)\( = \frac{{23}}{{23}}\)\( = 1\)

Câu 2 :

Tìm \(x\), biết:

a) x + 5,5 = 16,5

b) \(\frac{3}{5}x - \frac{1}{3} = \frac{7}{3}\)

Phương pháp giải :

Sử dụng các phép tính với số thập phân và phân số.

Lời giải chi tiết :

a) x + 5,5 = 16,5

x = 16,5 – 5,5

x = 11

Vậy x = 11.

b) \(\frac{3}{5}x - \frac{1}{3} = \frac{7}{3}\)