Đề thi vào 10 môn Toán Hải Phòng năm 2020

Lựa chọn câu để xem lời giải nhanh hơn

Đề bài
Lời giải chi tiết

Tải về

Đề bài

Bài 1:

Cho hai biểu thức: \(A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\) và \(B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\) với \(x > 0.\)

a) Rút gọn biểu thức \(A\) và biểu thức \(B.\)

b) Tìm các giá trị của \(x\) để giá trị của biểu thức \(A\) bằng ba lần giá trị của biểu thức \(B.\)

Bài 2:

a) Cho hàm số \(y = ax + b\) có đồ thị là đường thẳng \(\left( d \right)\). Xác định các giá trị của \(a\) và \(b\) biết \(\left( d \right)\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\) và \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\).

b) Giải hệ phương trình \(\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\).

Bài 3:

1. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).

a) Giải phương trình \(\left( 1 \right)\) với \(m = 7.\)

b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho biểu thức \(M = x_1^2 + x_2^2 - {x_1}{x_2}\) đạt giá trị nhỏ nhất.

2. Bài toán có nội dung thực tế:

Một nhà máy theo kế hoạch phải sản xuất 2100 thùng nước sát khuẩn trong một thời gian quy định (số thùng nước sát khuẩn nhà máy phải sản xuất trong mỗi ngày là bằng nhau). Để đẩy nhanh tiến độ công việc trong giai đoạn tăng cường phòng chống đại dịch COVID-19, mỗi ngày nhà máy đã sản xuất nhiều hơn dự định 35 thùng nước sát khuẩn. Do đó, nhà máy đã hoàn thành công việc trước thời hạn 3 ngày. Hỏi theo kế hoạch, mỗi ngày nhà máy sản xuất bao nhiêu thùng nước sát khuẩn?

Bài 4:

1. Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB\) và \(AC\) của đường tròn (\(B\) và \(C\) là các tiếp điểm). Gọi \(E\) là trung điểm của của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(EB\) với đường tròn \(\left( O \right)\), \(K\) là giao điểm của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(AF\) với đường tròn \(\left( O \right)\). Chứng minh:

a) Tứ giác \(ABOC\) là tứ giác nội tiếp và tam giác \(ABF\) đồng dạng với tam giác \(AKB\).

b) \(BF.CK = CF.BK\).

c) Tam giác \(FCE\) đồng dạng với tam giác \(CBE\) và \(EA\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).

2. Một hình nón có bán kính đáy là \(5\,cm,\) diện tích xung quanh bằng \(65\pi \,\,c{m^2}.\) Tính chiều cao của hình nón đó.

Bài 5:

a) Cho \(x,y\) là hai số thực bất kì. Chứng minh \({x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\)

b) Cho \(x,y,z\) là ba số thực dường thỏa mãn \(\sqrt x + \sqrt y + \sqrt z = 2\). Chứng minh

\(\dfrac{{x\sqrt x }}{{x + \sqrt {xy} + y}} + \dfrac{{y\sqrt y }}{{y + \sqrt {yz} + z}} + \dfrac{{z\sqrt z }}{{z + \sqrt {zx} + x}} \ge \dfrac{2}{3}\)

Lời giải chi tiết

Bài 1 (1,5 điểm)

Cách giải:

Cho hai biểu thức: \(A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\) và \(B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\) với \(x > 0.\)

a) Rút gọn biểu thức \(A\) và biểu thức \(B.\)

+) Rút gọn biểu thức \(A:\)

\(\begin{array}{l}A = 3\sqrt 7 - \sqrt {28} + \sqrt {175} - 3\\\,\,\,\,\, = 3\sqrt 7 - \sqrt {{2^2}.7} + \sqrt {{5^2}.7} - 3\\\,\,\,\,\, = 3\sqrt 7 - 2\sqrt 7 + 5\sqrt 7 - 3\\\,\,\,\,\, = 6\sqrt 7 - 3.\end{array}\)

+) Rút gọn biểu thức \(B:\)

Điều kiện: \(x > 0.\)

\(\begin{array}{l}B = \dfrac{{x - \sqrt x }}{{\sqrt x }} + \dfrac{{x + \sqrt x }}{{\sqrt x + 1}}\\\,\,\,\, = \dfrac{{\sqrt x \left( {\sqrt x - 1} \right)}}{{\sqrt x }} + \dfrac{{\sqrt x \left( {\sqrt x + 1} \right)}}{{\sqrt x + 1}}\\\,\,\,\, = \sqrt x - 1 + \sqrt x \\\,\,\,\, = 2\sqrt x - 1.\end{array}\)

Vậy với \(A = 6\sqrt 7 - 3\) và \(B = 2\sqrt x \) với \(x > 0.\)

b) Tìm các giá trị của \(x\) để giá trị của biểu thức \(A\) bằng ba lần giá trị của biểu thức \(B.\)

Điều kiện: \(x > 0.\)

Theo đề bài ta có:\(A = 3B\)

\(\begin{array}{l} \Leftrightarrow 6\sqrt 7 - 3 = 3.\left( {2\sqrt x - 1} \right)\\ \Leftrightarrow 6\sqrt 7 - 3 = 6\sqrt x - 3\\ \Leftrightarrow 6\sqrt x = 6\sqrt 7 \\ \Leftrightarrow \sqrt x = \sqrt 7 \\ \Leftrightarrow x = 7\,\,\,\left( {tm} \right)\end{array}\)

Vậy \(x = 7\) thì \(A = 3B.\)

Câu 2 (2,0 điểm)

Cách giải:

a) Cho hàm số \(y = ax + b\) có đồ thị là đường thẳng \(\left( d \right)\). Xác định các giá trị của \(a\) và \(b\) biết \(\left( d \right)\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\) và \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\).

Vì đường thẳng \(\left( d \right):\,\,y = ax + b\) song song với đường thẳng \(y = - \dfrac{1}{2}x + 2020\) nên: \(\left\{ \begin{array}{l}a = - \dfrac{1}{2}\\b \ne 2020\end{array} \right.\).

Khi đó phương trình đường thẳng \(\left( d \right)\) có dạng \(\left( d \right):\,\,y = - \dfrac{1}{2}x + b\), với \(b \ne 2020\).

Vì \(\left( d \right)\) cắt trục hoành tại điểm có hoành độ bằng \( - 5\) nên đường thẳng \(\left( d \right)\) đi qua điểm \(\left( { - 5;0} \right)\).

Thay tọa độ điểm \(\left( { - 5;0} \right)\) và phương trình đường thẳng \(\left( d \right)\) ta có:

\(0 = - \dfrac{1}{2}.\left( { - 5} \right) + b \Leftrightarrow 0 = \dfrac{5}{2} + b \Leftrightarrow b = - \dfrac{5}{2}\) (thỏa mãn).

Vậy \(a = - \dfrac{1}{2}\) và \(b = - \dfrac{5}{2}.\)

b) Giải hệ phương trình \(\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\).

Ta có:

\(\begin{array}{l}\,\,\,\,\,\left\{ \begin{array}{l}3\left( {x - 1} \right) + 2\left( {x - 2y} \right) = 10\\4\left( {x - 2} \right) - \left( {x - 2y} \right) = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}3x - 3 + 2x - 4y = 10\\4x - 8 - x + 2y = 2\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}5x - 4y = 13\\3x + 2y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}5x - 4y = 13\\6x + 4y = 20\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}11x = 33\\3x + 2y = 10\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\3.3 + 2y = 10\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x = 3\\2y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = \dfrac{1}{2}\end{array} \right.\end{array}\)

Vậy nghiệm của hệ phương trình là \(\left( {x;y} \right) = \left( {3;\dfrac{1}{2}} \right)\).

Bài 3 (2,5 điểm)

Cách giải:

1. Cho phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) (\(x\) là ẩn số, \(m\) là tham số).

a) Giải phương trình \(\left( 1 \right)\) với \(m = 7.\)

Với \(m = 7\) ta có phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\,{x^2} - 2\left( {7 + 1} \right)x + {7^2} - 1 = 0\,\,\,\,\\ \Leftrightarrow {x^2} - 16x + 48 = 0\\ \Leftrightarrow {x^2} - 4x - 12x + 48 = 0\\ \Leftrightarrow x\left( {x - 4} \right) - 12\left( {x - 4} \right) = 0\\ \Leftrightarrow \left( {x - 12} \right)\left( {x - 4} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 12 = 0\\x - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 12\\x = 4\end{array} \right..\end{array}\)

Vậy với \(m = 7\) thì phương trình có tập nghiệm là \(S = \left\{ {4;\,\,12} \right\}.\)

b) Xác định các giá trị của \(m\) để phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\) sao cho biểu thức \(M = x_1^2 + x_2^2 - {x_1}{x_2}\) đạt giá trị nhỏ nhất.

Phương trình \({x^2} - 2\left( {m + 1} \right)x + {m^2} - 1 = 0\,\,\,\,\,\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}\)

\(\begin{array}{l} \Leftrightarrow \Delta ' \ge 0\\ \Leftrightarrow {\left( {m + 1} \right)^2} - {m^2} + 1 \ge 0\\ \Leftrightarrow {m^2} + 2m + 1 - {m^2} + 1 \ge 0\\ \Leftrightarrow 2m + 2 \ge 0\\ \Leftrightarrow m \ge - 1.\end{array}\)

Với \(m \ge - 1\) thì phương trình \(\left( 1 \right)\) có hai nghiệm \({x_1},\,\,{x_2}.\)

Áp dụng hệ thức Vi-et ta có:\(\left\{ \begin{array}{l}{x_1} + {x_2} = 2\left( {m + 1} \right) = 2m + 2\\{x_1}{x_2} = {m^2} - 1\end{array} \right..\)

Theo đề bài ta có:

\(\begin{array}{l}M = x_1^2 + x_2^2 - {x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 2{x_1}{x_2} - {x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {{x_1} + {x_2}} \right)^2} - 3{x_1}{x_2}\\\,\,\,\,\,\,\,\, = {\left( {2m + 2} \right)^2} - 3\left( {{m^2} - 1} \right)\\\,\,\,\,\,\,\, = 4{m^2} + 8m + 4 - 3{m^2} + 3\\\,\,\,\,\,\,\, = {m^2} + 8m + 7\\\,\,\,\,\,\,\, = {m^2} + 8m + 16 - 9\\\,\,\,\,\,\,\, = {\left( {m + 4} \right)^2} - 9\end{array}\)

Với \(m \ge - 1\) \( \Rightarrow m + 4 \ge 3\) \( \Rightarrow {\left( {m + 4} \right)^2} \ge 9 \Rightarrow {\left( {m + 4} \right)^2} - 9 \ge 0\)

\( \Rightarrow Min\,\,M = 0\)

Dấu “=” xảy ra \( \Leftrightarrow m = - 1\,\,\,\left( {tm} \right).\)

Vậy \(m = - 1\) thỏa mãn điều kiện bài toán.

2. Bài toán có nội dung thực tế:

Gọi số thùng nước sát khuẩn mỗi ngày nhà máy sản xuất được theo kế hoạch là \(x\) (thùng), \(\left( {x < 2100,\,\,x \in {\mathbb{N}^*}} \right).\)

\( \Rightarrow \) Thời gian dự định nhà máy sản xuất xong 2100 thùng nước sát khuẩn là: \(\dfrac{{2100}}{x}\) (ngày).

Thực tế, mỗi ngày nhà máy sản xuất được số thùng nước sát khuẩn là: \(x + 35\) (thùng).

\( \Rightarrow \) Thời gian thực tế nhà máy sản xuất xong 2100 thùng nước sát khuẩn là: \(\dfrac{{2100}}{{x + 35}}\) (ngày).

Nhà máy đã hoàn thành xong công việc trước thời hạn 3 ngày nên ta có phương trình:

\(\begin{array}{l}\,\,\,\,\,\,\,\,\dfrac{{2100}}{x} - \dfrac{{2100}}{{x + 35}} = 3\\ \Leftrightarrow 2100\left( {x + 35} \right) - 2100x = 3x\left( {x + 35} \right)\\ \Leftrightarrow 2100x + 73500 - 2100x = 3{x^2} + 105x\\ \Leftrightarrow 3{x^2} + 105x - 73500 = 0\\ \Leftrightarrow {x^2} + 35x - 24500 = 0\\ \Leftrightarrow {x^2} + 175x - 140x - 24500 = 0\\ \Leftrightarrow x\left( {x + 175} \right) - 140\left( {x + 175} \right) = 0\\ \Leftrightarrow \left( {x + 175} \right)\left( {x - 140} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 175 = 0\\x - 140 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 175\,\,\,\left( {ktm} \right)\\x = 140\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy theo kế hoạch, mỗi ngày nhà máy sản xuất được 140 thùng nước sát khuẩn.

Bài 4 (3,5 điểm)

Cách giải:

1. Qua điểm \(A\) nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến \(AB\) và \(AC\) của đường tròn (\(B\) và \(C\) là các tiếp điểm). Gọi \(E\) là trung điểm của của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(EB\) với đường tròn \(\left( O \right)\), \(K\) là giao điểm của đoạn thẳng \(AC\), \(F\) là giao điểm thứ hai của đường thẳng \(AF\) với đường tròn \(\left( O \right)\). Chứng minh:

a) Tứ giác \(ABOC\) là tứ giác nội tiếp và tam giác \(ABF\) đồng dạng với tam giác \(AKB\).

Ta có: \(AB,\,\,AC\) là hai tiếp tuyến của \(\left( O \right)\) tại \(B,\,\,C\)

\( \Rightarrow \left\{ \begin{array}{l}OB \bot AB\\OB \bot AC\end{array} \right.\) \( \Rightarrow \angle ABO = \angle ACO = {90^0}\)

Xét tứ giác \(ABOC\) ta có:

\(\angle ABO + \angle ACO = {90^0} + {90^0} = {180^0}\)

Mà hai góc này là hai góc đối diện

\( \Rightarrow ABOC\) là tứ giác nội tiếp (dhnb). (đpcm)

Xét \(\Delta ABF\) và \(\Delta AKB\) ta có:

\(\angle A\) chung

\(\angle AKB = \angle ABF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BF\))

\( \Rightarrow \Delta ABF \sim \Delta AKB\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\)

b) \(BF.CK = CF.BK\).

Ta có: \(\Delta ABF \sim \Delta AKB\,\,\,\left( {cmt} \right)\)

\( \Rightarrow \dfrac{{AB}}{{AK}} = \dfrac{{BF}}{{KB}} = \dfrac{{AF}}{{AB}}\) (các cặp cạnh tương ứng tỉ lệ).

Xét \(\Delta ACF\) và \(\Delta AKC\) ta có:

\(\angle A\) chung

\(\angle AKC = \angle ACF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(CF\))

\( \Rightarrow \Delta ACF \sim \Delta AKC\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\)

\( \Rightarrow \dfrac{{AC}}{{AK}} = \dfrac{{CF}}{{KC}} = \dfrac{{AF}}{{AC}}\) (các cặp cạnh tương ứng tỉ lệ).

Mà \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)

\(\begin{array}{l} \Rightarrow \dfrac{{AB}}{{AK}} = \dfrac{{AC}}{{AK}} = \dfrac{{BF}}{{KB}} = \dfrac{{CF}}{{KC}}\\ \Rightarrow BF.KC = KB.CF\,\,\,\,\left( {dpcm} \right).\end{array}\)

c) Tam giác \(FCE\) đồng dạng với tam giác \(CBE\) và \(EA\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).

Ta có: \(\angle BKC = \angle BCE\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(BC\))

Lại có: \(BFCK\) là tứ giác nội tiếp đường tròn \(\left( O \right)\)

\( \Rightarrow \angle EFC = \angle BKC\) (góc ngoài tại 1 đỉnh bằng góc trong tại đỉnh đối diện)

\( \Rightarrow EFC = \angle BCE\,\,\left( { = \angle BKC} \right)\)

Xét \(\Delta FCE\) và \(\Delta CBE\) ta có:

\(\begin{array}{l}\angle E\,\,\,chung\\\angle EFC = \angle ECB\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta FCE \sim \Delta CBE\,\,\,\left( {g - g} \right)\,\,\,\left( {dpcm} \right).\end{array}\)

Vì \(\Delta FCE = \angle CBE\,\,\,\left( {cmt} \right)\)

\(\begin{array}{l} \Rightarrow \dfrac{{FE}}{{CE}} = \dfrac{{CE}}{{BE}} \Rightarrow C{E^2} = FE.BE = A{E^2}\\ \Rightarrow \dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\end{array}\)

Xét \(\Delta AEF\) và \(\Delta BEA\) ta có:

\(\begin{array}{l}\angle AEB\,\,\,chung\\\dfrac{{EA}}{{EB}} = \dfrac{{EF}}{{EA}}\,\,\left( {cmt} \right)\\ \Rightarrow \Delta AEF \sim \Delta BEA\,\,\,\left( {c - g - c} \right)\end{array}\)

\( \Rightarrow \angle FAE = \angle ABE\) (hai góc tương ứng)

Mà \(\angle ABE\) là góc nội tiếp chắn cung \(BF\) của đường tròn ngoại tiếp \(\Delta ABF\)

\(\angle FAE\) được tạo bởi dây cung \(AF\) và \(AE\)(\(E\) nằm ngoài đường tròn)

\( \Rightarrow AE\) là tiếp tuyến của đường tròn ngoại tiếp \(\Delta ABF.\) (đpcm)

2. Một hình nón có bán kính đáy là \(5\,cm,\) diện tích xung quanh bằng \(65\pi \,\,c{m^2}.\) Tính chiều cao của hình nón đó.

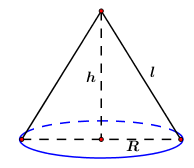
Ta có: \({S_{xq}} = \pi Rl\) \( \Leftrightarrow 5\pi l = 65\pi \)\( \Leftrightarrow l = \dfrac{{65\pi }}{{5\pi }} = 13\,\,cm.\)

Áp dụng định lý Pitago ta có chiều cao của hình nón là: \(h = \sqrt {{l^2} - {R^2}} = \sqrt {{{13}^2} - {5^2}} = 12\,\,cm.\)

Bài 5 (1,0 điểm)

Cách giải:

a) Cho \(x,y\) là hai số thực bất kì. Chứng minh \({x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\)

Ta có:

\(\begin{array}{l}{x^2} - xy + {y^2} \ge \dfrac{1}{3}\left( {{x^2} + xy + {y^2}} \right)\\ \Leftrightarrow 3{x^2} - 3xy + 3{y^2} \ge {x^2} + xy + {y^2}\\ \Leftrightarrow 2{x^2} - 4xy + 2{y^2} \ge 0\\ \Leftrightarrow {x^2} - 2xy + {y^2} \ge 0\end{array}\)

\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) (luôn đúng)

Dấu “=” xảy ra khi \(x = y\).

Vậy ta có đpcm.

b) Cho \(x,y,z\) là ba số thực dường thỏa mãn \(\sqrt x + \sqrt y + \sqrt z = 2\). Chứng minh

\(\dfrac{{x\sqrt x }}{{x + \sqrt {xy} + y}} + \dfrac{{y\sqrt y }}{{y + \sqrt {yz} + z}} + \dfrac{{z\sqrt z }}{{z + \sqrt {zx} + x}} \ge \dfrac{2}{3}\)

Đặt \(\left\{ \begin{array}{l}a = \sqrt x > 0\\b = \sqrt y > 0\\c = \sqrt z > 0\end{array} \right. \Rightarrow a + b + c = 2\) ta được:

\(\begin{array}{l}VT = \dfrac{{{a^3}}}{{{a^2} + ab + {b^2}}} + \dfrac{{{b^3}}}{{{b^2} + bc + {c^2}}} + \dfrac{{{c^3}}}{{{c^2} + ca + {a^2}}}\\ = \dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\end{array}\)

Áp dụng BĐT \(\dfrac{{{a^2}}}{x} + \dfrac{{{b^2}}}{y} \ge \dfrac{{{{\left( {a + b} \right)}^2}}}{{x + y}}\) ta có:

\(\begin{array}{l}\dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} \ge \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right)}}\\ \Rightarrow \dfrac{{{a^4}}}{{{a^3} + {a^2}b + a{b^2}}} + \dfrac{{{b^4}}}{{{b^3} + {b^2}c + b{c^2}}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right)}} + \dfrac{{{c^4}}}{{{c^3} + {c^2}a + c{a^2}}}\\ \ge \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{\left( {{a^3} + {a^2}b + a{b^2}} \right) + \left( {{b^3} + {b^2}c + b{c^2}} \right) + \left( {{c^3} + {c^2}a + c{a^2}} \right)}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{{a^3} + {a^2}b + {a^2}c + {b^3} + {b^2}a + {b^2}c + {c^3} + {c^2}a + {c^2}b}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{{a^2}\left( {a + b + c} \right) + {b^2}\left( {a + b + c} \right) + {c^2}\left( {a + b + c} \right)}}\\ = \dfrac{{{{\left( {{a^2} + {b^2} + {c^2}} \right)}^2}}}{{\left( {{a^2} + {b^2} + {c^2}} \right)\left( {a + b + c} \right)}}\\ = \dfrac{{{a^2} + {b^2} + {c^2}}}{{a + b + c}}\\ = \dfrac{1}{2}\left( {\dfrac{{{a^2}}}{1} + \dfrac{{{b^2}}}{1} + \dfrac{{{c^2}}}{1}} \right)\\ \ge \dfrac{1}{2}.\dfrac{{{{\left( {a + b + c} \right)}^2}}}{{1 + 1 + 1}} = \dfrac{1}{2}.\dfrac{{{2^2}}}{3} = \dfrac{2}{3}\end{array}\)

\( \Rightarrow \dfrac{{{a^3}}}{{{a^2} + ab + {b^2}}} + \dfrac{{{b^3}}}{{{b^2} + bc + {c^2}}} + \dfrac{{{c^3}}}{{{c^2} + ca + {a^2}}} \ge \dfrac{2}{3}\) (đpcm)

Dấu “=” xảy ra khi \(a = b = c = \dfrac{2}{3}\).

Bài trước Bài sau