Diện tích xung quanh hình chóp tứ giác đều

1. Lý thuyết

 

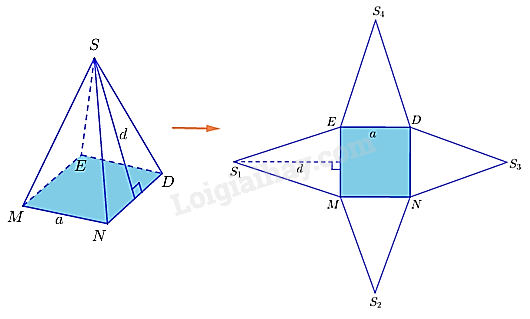
+ Diện tích xung quanh của hình chóp tứ giác đều bằng nữa tích của chu vi đáy với độ dài trung đoạn.

+ Công thức tổng quát :  \({S_{xq}} = \frac{1}{2}.C.d\) . Với :

+ \({S_{xq}}\) : Diện tích xung quanh của hình chóp tứ giác đều.

+ Chu vi đáy : C = 4.a   (a là độ dài cạnh đáy hình vuông).

+ d: Độ dài trung đoạn của hình chóp tứ giác đều.

2. Ví dụ minh họa

Cho hình chóp tứ giác đều S.ABCD với kích thước như hình vẽ.

a) Tính chu vi đáy ABCD.

b) Cho biết độ dài trung đoạn hình chóp  S.ABC.

c) Tính diện tích xung quanh của hình chóp tứ giác đều S.ABCD.

Lời giải:

a) Chu vi tam giác ABC là: C = 4a = 4.10 = 40 (cm).

b) Độ dài trung đoạn hình chóp  S.ABC là d = SI = 12 (cm)

c) Diện tích xung quanh của hình chóp tam giác đều S.ABC là :

                              \({S_{xq}} = \frac{1}{2}.C.d = \frac{1}{2}.40.12 = 240(c{m^2})\)