Giải bài 1.34 trang 25 sách bài tập toán 12 - Kết nối tri thức
Đề bài
Cho hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right)\) xác định trên \(\mathbb{R}\) và \(f'\left( x \right)\) có đồ thị như hình vẽ sau:
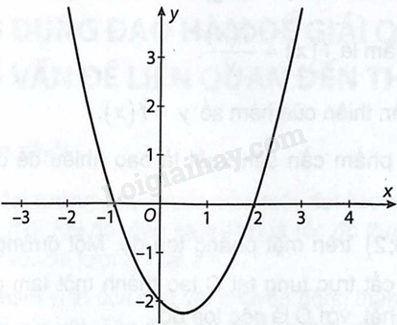
Tìm các khoảng đồng biến, khoảng nghịch biến và các điểm cực trị của hàm số \(y = f\left( x \right)\).
Phương pháp giải - Xem chi tiết
+ Từ đồ thị của đạo hàm tìm \(x\) để đạo hàm bằng \(0\) (các giao điểm của đồ thị và trục
hoành).
+ Xét dấu đạo hàm (quan sát đồ thị, phần đồ thị phía trên trục hoành nhận giá trị dương, dưới trục hoành nhận giá trị âm, xác định các khoảng của x thỏa mãn từng phần). Từ đó xác định các khoảng đồng biến, nghịch biến.
+ Lập bảng biến thiên. Từ bảng biến thiên suy ra cực trị.
Lời giải chi tiết
Từ đồ thị của hàm \(f'\left( x \right)\) ta có \(f'\left( x \right) = 0 \Leftrightarrow x = - 1\) hoặc \(x = 2\).
Ta có \(f'\left( x \right) > 0\) với mọi \(x \in \left( { - \infty ; - 1} \right)\) và \(x \in \left( {2; + \infty } \right)\) do đó \(f\left( x \right)\) đồng biến trên từng khoảng \(\left( { - \infty ; - 1} \right)\) và \(\left( {2; + \infty } \right)\); \(f'\left( x \right) < 0\) với mọi \(x \in \left( { - 1;2} \right)\) do đó \(f\left( x \right)\) nghịch biến trên \(\left( { - 1;2} \right)\).
Lập bảng biến thiên
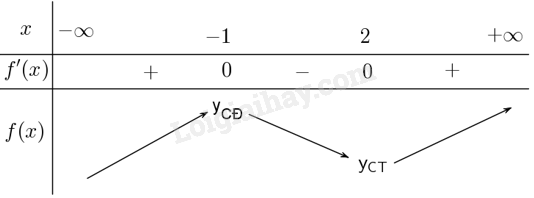
Hàm số đạt cực đại tại \(x = - 1\), đạt cực tiểu tại \(x = 2\).
- Giải bài 1.35 trang 25 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 1.36 trang 26 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 1.37 trang 26 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 1.38 trang 26 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 1.39 trang 26 sách bài tập toán 12 - Kết nối tri thức

