Giải bài 16 trang 130 sách bài tập toán 9 - Cánh diều tập 2
Đề bài
Khi quay tam giác OHA vuông cân ở H một vòng xung quanh đường thẳng cố định OH, ta được một hình nón như ở Hình 14. Hỏi diện tích xung quanh của hình nón đó là bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)? Biết diện tích tam giác OHA là 4 cm2.
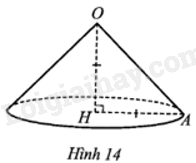
Phương pháp giải - Xem chi tiết
Dựa vào: Diện tích xung quanh hình nón: \({S_{xq}} = \pi rl\).
Lời giải chi tiết
Ta có diện tích của tam giác OHA vuông tại H là \(\frac{1}{2}OH.HA\) (cm2).
Theo bài, tam giác OHA vuông cân tại H có diện tích bằng 4 cm2 nên
\(\frac{1}{2}OH.HA = 4\). Suy ra OH. HA = 8.
Do đó OH = HA = \(2\sqrt 2 \) (cm) (do ∆OHA vuông cân tại H).
Xét ∆OHA vuông tại H, theo định lí Pythagore, ta có: OA2 = OH2 + HA2
Suy ra \(OA = \sqrt {{{\left( {2\sqrt 2 } \right)}^2} + {{\left( {2\sqrt 2 } \right)}^2}} = \sqrt {8 + 8} = \sqrt {16} = 4\) (cm).
Vậy diện tích xung quanh của hình nón đó là:
\(\pi .HA.OA = \pi .2\sqrt 2 .4 = 8\sqrt 2 \pi \approx 36\) (cm2).

