Giải bài 3 trang 36 Chuyên đề học tập Toán 12 - Cánh diều
Đề bài
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh vật học thấy rằng: Nếu trên mỗi đơn vị diện tích của mặt hồ có \(n\) con cá sau một vụ cân nặng:
\(P(n) = 480 - 20n\) (gam)
Hỏi phải thả bao nhiêu cá trên một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.
Phương pháp giải - Xem chi tiết
+) Tìm biểu thức biểu diễn khối lượng cá thu hoạch được sau một vụ là \(n.P(n)\)
+) Xét hàm số \(f(n) = nP(n)\), yêu cầu bài toán đồng nghĩ với việc ta sẽ đi tìm giá trị lớn nhất của hàm số \(f(n)\) khi \(0 < n < 24.\)
Lời giải chi tiết
Khối lượng cá thu hoạch được sau một vụ là
\(n.P(n) = n.(480 - 20n) = 480n - 20{n^2}\) (gam)
Xét hàm số \(f(n) = 480n - 20{n^2}\) với \(0 < n < 24.\)
Ta có \(f'(n) = 480 - 40n.\)
Do đó \(f'(n) = 0 \Leftrightarrow n = 12.\)
Ta có bảng biến thiên hàm số \(f(n)\) như sau:
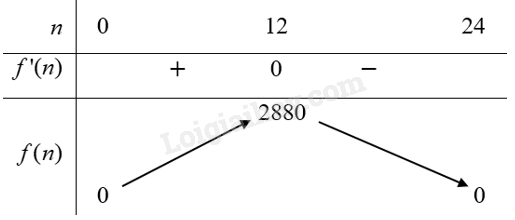
Căn cứ vào bảng biến thiên ta có \(\mathop {\max }\limits_{(0;24)} f(n) = f(12) = 2880\) tại \(n = 12.\)
Vậy phải thả 12 con cá trên cùng một đơn vị diện tích của mặt hồ để sau một vụ thu hoạch được nhiều cá nhất.

