Giải bài 30 trang 95 sách bài tập Toán 6 – Cánh Diều Tập 2

Đề bài

a) Vẽ đoạn thẳng AB có độ dài 8 cm và trung điểm C của đoạn thẳng đó.

b) Vẽ các điểm P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB

c) Tính độ dài các đoạn thẳng AP, QB và PQ.

Phương pháp giải - Xem chi tiết

Trung điểm O của đoạn thẳng AB là điểm nằm giữa A và B sao cho \(OA = OB\)

Nếu O là trung điểm của đoạn thẳng AB thì \(OA = OB = \frac{{AB}}{2}\)

Lời giải chi tiết

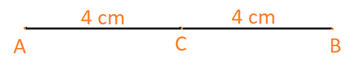
a) Đoạn thẳng AB có độ dài 8 cm và C là trung điểm của đoạn thẳng đó.

Vì C là trung điểm AB nên \(CA = CB = \frac{{AB}}{2} = \frac{8}{2}= 4\,cm\)

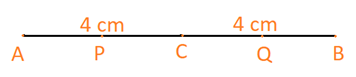
b) P, Q lần lượt là trung điểm của các đoạn thẳng AC và CB

c) Ta có:

P là trung điểm AC nên \(PA = PC = \frac{{AC}}{2} = \frac{4}{2}= 2\,cm\)

Q là trung điểm BC nên \(QB = QC = \frac{{BC}}{2} = \frac{4}{2}=2\,cm\)

Mà: \(PQ = PC + CQ\)(vì C nằm giữa P và Q)

\( \Rightarrow PQ = 2 + 2 = 4\,(cm)\)

Vậy \(AP = 2\,cm;\;QB = 2\,cm;\;PQ = 4\,cm\)

Bài trước Bài sau