-
Toán 8 tập 1

-
Toán 8 tập 2

-
 Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
-
 Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
- Bài 1. Định lí Thalès
- Bài 2. Đường trung bình của tam giác
- Bài 3. Tính chất đường phân giác trong của tam giác
- Bài 4. Tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng cạnh - cạnh - cạnh
- Bài 6. Trường hợp đồng dạng cạnh - góc - cạnh
- Bài 7. Trường hợp đồng dạng góc - góc
- Bài 8. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 9. Hình đồng dạng
- Ôn tập chương 6
-
 Chương 7 Một số yếu tố thống kê và xác suất
Chương 7 Một số yếu tố thống kê và xác suất
-
Giải bài 3.3 trang 58 SGK Toán 8 - Cùng khám phá
Đề bài
Cho tam giác ABC có \(AB = 9cm,AC = 12cm,BC = 15cm.\)
a) Chứng minh tam giác ABC vuông tại A.
b) Trên tia đối của tia AB, lấy điểm D sao cho \(AD = 5cm.\) Tính độ dài CD.
Phương pháp giải - Xem chi tiết
a) Sử dụng định lí Pythagore đảo
b) Sử dụng định lí Pythagore để tính độ dài CD.
Lời giải chi tiết
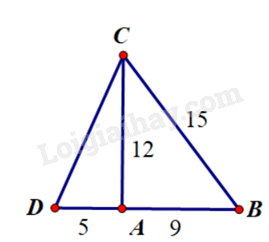
a) Ta có \(A{B^2} + A{C^2} = {9^2} + {12^2} = 225 = {15^2} = B{C^2}\)
Tam giác ABC vuông tại A (định lí Pythagore đảo).
b) Xét tam giác ABC vuông tại A suy ra \(AC \bot BD \Rightarrow \widehat {DAC} = {90^0}\)
Xét tam giác ADC vuông tại A có:
\(A{D^2} + A{C^2} = D{C^2}\)(định lí Pythagore)
\( \Rightarrow DC = \sqrt {{{12}^2} + {5^2}} = 13cm.\)