Giải bài 4 trang 63 sách bài tập toán 12 - Chân trời sáng tạo

Đề bài

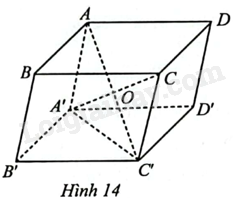
Cho hình hộp \(ABCD.A'B'C'D'\) có \(AC'\) và \(A'C\) cắt nhau tại \(O\). Cho biết \(AO = a\). Tính theo \(a\) độ dài các vectơ:

 

a) \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'} \);

b) \(\overrightarrow {C'B'}  + \overrightarrow {C'D'}  + \overrightarrow {A'A} \).

Lời giải chi tiết

a) Theo quy tắc hình hộp ta có: \(\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'}  = \overrightarrow {AC'} \).

Do đó \(\left| {\overrightarrow {AB}  + \overrightarrow {AD}  + \overrightarrow {AA'} } \right| = \left| {\overrightarrow {AC'} } \right| = AC' = 2AO = 2{\rm{a}}\).

b) Theo quy tắc hình hộp ta có: \(\overrightarrow {C'B'}  + \overrightarrow {C'D'}  + \overrightarrow {A'A}  = \overrightarrow {C'B'}  + \overrightarrow {C'D'}  + \overrightarrow {C'C}  = \overrightarrow {C'A} \).

Do đó \(\left| {\overrightarrow {C'B'}  + \overrightarrow {C'D'}  + \overrightarrow {A'A} } \right| = \left| {\overrightarrow {C'A} } \right| = C'A = 2AO = 2{\rm{a}}\).