- Trang chủ
- Lớp 8
- Toán học Lớp 8
- SGK Toán - Kết nối tri thức Lớp 8
- Toán 8 tập 1 với cuộc sống
- Chương 4 Định lí Thales
-
Toán 8 tập 1 với cuộc sống

-
Toán 8 tập 2

Giải bài 4.2 trang 80 SGK Toán 8 tập 1 - Kết nối tri thức
Đề bài
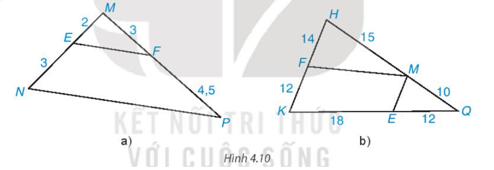
Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Áp dụng định lí Thalès đảo, từ các tỉ lệ thức, ta suy ra hai đường thẳng song song với nhau.
Lời giải chi tiết
• Hình 4.10a)
Ta có: \(\dfrac{{EM}}{{EN}} = \dfrac{2}{3};\dfrac{{MF}}{{PF}} = \dfrac{3}{{4,5}} = \dfrac{2}{3}\) nên \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\)
Vì \(\dfrac{{EM}}{{EN}} = \dfrac{{MF}}{{PF}}\), E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.
• Hình 4.10b)
* Ta có: \(\dfrac{{HF}}{{KF}} = \dfrac{{14}}{{12}} = \dfrac{7}{6};\dfrac{{HM}}{{MQ}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\)
Vì \(\dfrac{{HF}}{{KF}} \ne \dfrac{{HM}}{{MQ}}\) nên MF không song song với KQ.
* Ta có: \(\dfrac{{MQ}}{{MH}} = \dfrac{{10}}{{15}} = \dfrac{2}{3};\dfrac{{EQ}}{{EK}} = \dfrac{{12}}{{18}} = \dfrac{2}{3}\)
Vì \(\dfrac{{MQ}}{{MH}} = \dfrac{{EQ}}{{EK}}\); F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.