Giải bài 4.22 trang 89 SGK Toán 8 tập 1 - Kết nối tri thức

Đề bài

Cho tam giác ABC cân tại A có AB = 15 cm, BC = 10 cm, đường phân giác trong của góc B cắt AC tại D. Khi đó, đoạn thẳng AD có độ dài là

A. 3 cm.

B. 6 cm.

C. 9 cm.

D. 12 cm.

Lời giải chi tiết

Đáp án đúng là: C

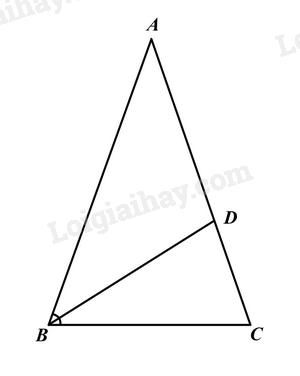
Vì tam giác ABC cân tại A nên AB = AC = 15 cm.

Theo đề bài, BD là tia phân giác của \(\widehat {ABC}\), áp dụng tính chất đường phân giác vào tam giác ABC, ta có:

\(\dfrac{{AB}}{{BC}} = \dfrac{{A{{D}}}}{{C{{D}}}} = \dfrac{{15}}{{10}} = \dfrac{3}{2}\) suy ra \(\dfrac{{A{{D}}}}{3} = \dfrac{{C{{D}}}}{2}\)

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

\(\dfrac{{A{{D}}}}{3} = \dfrac{{C{{D}}}}{2} = \dfrac{{A{{D}} + C{{D}}}}{{3 + 2}} = \dfrac{{AC}}{5} = \dfrac{{15}}{5} = 3\)

Do đó AD = 3 . 3 = 9 (cm).

Vậy AD = 9 cm.