- Trang chủ
- Lớp 7
- Toán học Lớp 7
- SGK Toán Lớp 7 Chân trời sáng tạo
- Toán 7 tập 1 Chân trời sáng tạo
- Chương 4. Góc và đường thẳng song song
-
GIẢI SGK TOÁN 8 CHÂN TRỜI SÁNG TẠO - MỚI NHẤT

-
Toán 7 tập 1

-
 Chương 1. Số hữu tỉ
Chương 1. Số hữu tỉ
-
 Chương 2. Số thực
Chương 2. Số thực
-
 Chương 3. Các hình khối trong thực tiễn
Chương 3. Các hình khối trong thực tiễn
- Bài 1. Hình hộp chữ nhật. Hình lập phương
- Bài 2. Diện tích xung quanh và thể tích của hình hộp chữ nhật, hình lập phương
- Bài 3. Hình lăng trụ đứng tam giác. Hình lăng trụ đứng tứ giác
- Bài 4. Diện tích xung quanh và thể tích của hình lăng trụ đứng tam giác, lăng trụ đứng tứ giác
- Bài 5. Hoạt động thực hành và trải nghiệm: Các bài toán về đo đạc và gấp hình
- Bài tập cuối chương 3
-
 Chương 4. Góc và đường thẳng song song
Chương 4. Góc và đường thẳng song song
-
 Chương 5. Một số yếu tố thống kê
Chương 5. Một số yếu tố thống kê
-
-
Toán 7 tập 2

-
 Chương 6. Các đại lượng tỉ lệ
Chương 6. Các đại lượng tỉ lệ
-
 Chương 7. Biểu thức đại số
Chương 7. Biểu thức đại số
-
 Chương 8. Tam giác
Chương 8. Tam giác
- Bài 1. Góc và cạnh của một tam giác
- Bài 2. Tam giác bằng nhau
- Bài 3. Tam giác cân
- Bài 4. Đường vuông góc và đường xiên
- Bài 5. Đường trung trực của một đoạn thẳng
- Bài 6. Tính chất ba đường trung trực của tam giác
- Bài 7. Tính chất ba đường trung tuyến của tam giác
- Bài 8. Tính chất ba đường cao của tam giác
- Bài 9. Tính chất ba đường phân giác của tam giác
- Bài 10. Hoạt động thực hành và trải nghiệm: Làm giàn hoa tam giác để trang trí lớp học
- Bài tập cuối chương 8
-
 Chương 9. Một số yếu tố xác suất
Chương 9. Một số yếu tố xác suất
-
Giải bài 5 trang 80 SGK Toán 7 tập 1 - Chân trời sáng tạo
Đề bài
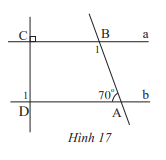
Cho Hình 17, biết a // b.
Tính số đo các góc \(\widehat {{B_1}}\) và \(\widehat {{D_1}}\)
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
*2 góc kề bù có tổng số đo là 180 độ
*Sử dụng tính chất 2 đường thẳng song song:
Một đường thẳng cắt hai đường thẳng song song thì:
+ 2 góc so le trong bằng nhau
+ 2 góc đồng vị bằng nhau
Lời giải chi tiết
Cách 1: Vì a//b, a \( \bot \) CD nên b \( \bot \) CD. Do đó, \(\widehat {{D_1}}=90^\circ \).
Vì a//b nên \(\widehat {{A_1}} + \widehat {{B_1}}=180^0\) (2 góc trong cùng phía) nên \(\widehat {{B_1}} + 70^\circ = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 70^\circ = 110^\circ \)
Vậy \(\widehat {{B_1}} =110^0; \widehat {{D_1}}=90^\circ \).
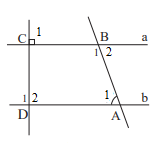
Cách 2: Vì a // b nên
+) \(\widehat {{C_1}} = \widehat {{D_2}}\) ( 2 góc đồng vị), mà \(\widehat {{C_1}} = 90^\circ \) nên \(\widehat {{D_2}} = 90^\circ \). Do đó, b\( \bot \) CD nên \(\widehat {{D_1}}=90^\circ \)
+) \(\widehat {{A_1}} = \widehat {{B_2}}\) ( 2 góc so le trong) nên \(\widehat {{B_2}} = 70^\circ \)
Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \)( 2 góc kề bù) nên \(\widehat {{B_1}} + 70^\circ = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 70^\circ = 110^\circ \).
Vậy \(\widehat {{B_1}} =110^0; \widehat {{D_1}}=90^\circ \).