Giải bài 6 trang 85 SGK Toán 8 – Cánh diều

Đề bài

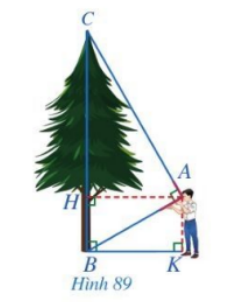
Trong Hình 89, bạn Minh dùng một dụng cụ để đo chiều cao của cây. Cho biết khoảng cách từ mắt bạn Minh đến cây và đến mặt đất lần lượt là \(AH = 2,8m\) và \(AK = 1,6m\). Em hãy tính chiều cao của cây.

Lời giải chi tiết

Xét tứ giác AHBK có \(\widehat H = \widehat B = \widehat K = 90^\circ \) nên AHBK là hình chữ nhật.

\( \Rightarrow AK = BH = 1,6m\)

Xét tam giác ABH vuông tại H có:

\(A{H^2} + H{B^2} = A{B^2}\) (Định lý Pytago)

\(\begin{array}{l} \Rightarrow 2,{8^2} + 1,{6^2} = A{B^2}\\ \Rightarrow A{B^2} = 10,4\\ \Rightarrow AB = \frac{{2\sqrt {65} }}{5}\end{array}\)

Xét tam giác ABC và tam giác HBA có:

\(\widehat {BAC} = \widehat {BHA} = 90^\circ \) và \(\widehat C\) chung

\( \Rightarrow \Delta ABC \backsim \Delta HBA\) (g-g)

\( \Rightarrow \frac{{BC}}{{BA}} = \frac{{AB}}{{HB}} \Leftrightarrow BC = A{B^2}:HB = {\left( {\frac{{2\sqrt {65} }}{5}} \right)^2}:1,6 = 6,5\)

Vậy cây cao 6,5m.