- Trang chủ
- Lớp 8
- Toán học Lớp 8
- SGK Toán Lớp 8
- Toán 8 tập 2
- Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
-
Toán 8 tập 1

-
Toán 8 tập 2

-
 Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
-
 Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
- Bài 1. Định lí Thalès
- Bài 2. Đường trung bình của tam giác
- Bài 3. Tính chất đường phân giác trong của tam giác
- Bài 4. Tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng cạnh - cạnh - cạnh
- Bài 6. Trường hợp đồng dạng cạnh - góc - cạnh
- Bài 7. Trường hợp đồng dạng góc - góc
- Bài 8. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 9. Hình đồng dạng
- Ôn tập chương 6
-
 Chương 7 Một số yếu tố thống kê và xác suất
Chương 7 Một số yếu tố thống kê và xác suất
-
Giải bài 6.43 trang 78 SGK Toán 8 - Cùng khám phá
Đề bài
Tính độ dài \(AF\) và \(EF\) trong Hình 6.112.
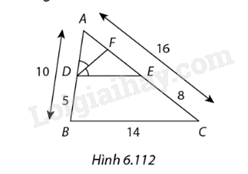
Phương pháp giải - Xem chi tiết
Áp dụng các trường hợp đồng dạng của tam giác và tính chất đường phân giác để tìm độ dài \(AF\) và \(EF\) .
Lời giải chi tiết
Ta có:
\(\begin{array}{l}AD = 10 - 5\\AE = 16 - 8 = 8\end{array}\)
Xét tam giác \(ABC\) và tam giác \(ADE\) , ta có:
\(\widehat A\) là góc chung
\(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{1}{2}\)
=> \(\Delta ABC\) ∽ \(\Delta ADE\) (c-g-c)
Ta có tỉ lệ đồng dạng:
\(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}} \Rightarrow \frac{{AD}}{{DE}} = \frac{{AB}}{{BC}} \\ \frac{{AD}}{{DE}} = \frac{{10}}{{14}} = \frac{5}{7}\)
Lại có:
\(\widehat {ADF} = \widehat {FDE}\)
=> \(DF\) là tia phân giác của tam giác \(ADE\)
Áp dụng tính chất tia phân giác ta có:
\(\frac{{AD}}{{DE}} = \frac{{AF}}{{FE}}\)
=> \(\frac{{AF}}{{FE}} = \frac{5}{7}\)
Mà \(AE = 8 = > AF = \frac{{10}}{3};FE = \frac{{14}}{3}\)