Giải bài 8 trang 12 Chuyên đề học tập Toán 12 - Cánh diều
Đề bài
Có hai nhóm học sinh. Nhóm thứ nhất có 5 nam và 6 nữ. Nhóm thứ hai có 5 nam và 7 nữ. Từ mỗi nhóm học sinh, ta chọn ngẫu nhiên 1 học sinh. Gọi X là số học sinh nữ trong số 2 học sinh được chọn ra.
a) Lập bảng phân bố xác suất của biến ngẫu nhiên rời rạc X.
b) Tính kì vọng, phương sai của X.
Phương pháp giải - Xem chi tiết
a) Gọi \(X = 0;X = 1;X = 2\)lần lượt là biến cố: “không có HS nữ được chọn”; “ có 1 HS nữ trong 2 HS được chọn”; “chọn được 2 HS nữ.”
Tính \(P(X = 0);P(X = 1);P(X = 2)\)
Lập bảng phân bố xác suất.
b) Áp dụng công thức:
Kì vọng: \(E(X) = {x_1}{p_1} + {x_2}{p_2} + ... + {x_n}{p_n}\)
Phương sai: \(V(X) = {({x_1} - \mu )^2}{p_1} + {({x_2} - \mu )^2}{p_2} + ... + {({x_n} - \mu )^2}{p_n}\)
Lời giải chi tiết
a) X là biến ngẫu nhiên rời rạc và nhận giá trị trong tập \(\left\{ {0;1;2} \right\}\)
Ta có \(n(\Omega ) = C_{11}^1.C_{12}^1 = 132\)
+ Biến cố X=0 là biến cố :”Không có học sinh nữ được chọn.”
Suy ra \(n(X = 0) = C_5^1.C_5^1 = 25 \Rightarrow P(X = 0) = \frac{{25}}{{132}}.\)
+ Biến cố X=1 là biến cố :”Có 1 học sinh nữ trong số 2 hs được chọn.”
TH1: Nhóm 1 chọn được học sinh nữ, nhóm 2 chọn được học sinh nam
Suy ra có \(C_6^1.C_5^1 = 30\) cách chọn
TH2: Nhóm 1 chọn được học sinh nam, nhóm 2 chọn được học sinh nữ.
Suy ra có \(C_5^1.C_7^1 = 35\) cách chọn
Do đó \(P(X = 1) = \frac{{30 + 35}}{{132}} = \frac{{65}}{{132}}\)
+ Biến cố X=2 là biến cố :”Chọn được 2 HS nữ.”
Suy ra \(n(X = 2) = C_6^1.C_7^1 = 42 \Rightarrow P(X = 2) = \frac{{42}}{{132}}.\)
Bảng phân bố xác suất của X là:
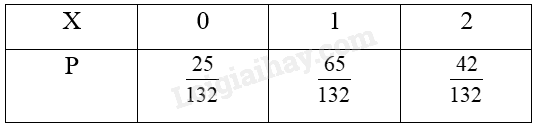
b) Có:
\(\begin{array}{l}E(X) = 0.\frac{{25}}{{132}} + 1.\frac{{65}}{{132}} + 2.\frac{{42}}{{132}} = \frac{{49}}{{132}}\\V(X) = {\left( {0 - \frac{{49}}{{132}}} \right)^2}.\frac{{25}}{{132}} + {\left( {1 - \frac{{49}}{{132}}} \right)^2}.\frac{{65}}{{132}} + {\left( {2 - \frac{{49}}{{132}}} \right)^2}.\frac{{42}}{{132}} \approx 0,49\end{array}\)

