Giải bài 9 trang 121 SGK Toán 8 tập 1 - Cánh diều

Đề bài

Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.

Lời giải chi tiết

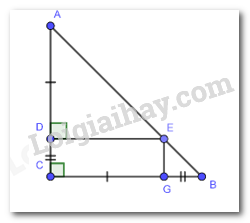
Vì \(\Delta ABC\) vuông cân tại C.

\( \Rightarrow \widehat {C{\rm{AB}}} = {45^0} \Rightarrow \widehat {DA{\rm{E}}} = {45^0}\)

\(\Rightarrow \widehat {DE{\rm{A}}} = {45^0} \Rightarrow \Delta ADE\) là tam giác vuông cân tại D

Suy ra AD = DE (1)

Mà: AD = CG (2)

Từ (1), (2) suy ra: DE = CG.

Mặt khác DE//CG (vì cùng vuông góc với AC)

Suy ra tứ giác CDEG là hình bình hành

Mặt khác: \(\widehat {DCG} = {90^0}\)

Suy ra hình bình hành CDEG là hình chữ nhật