Giải bài 9.9 trang 53 sách bài tập toán 9 - Kết nối tri thức tập 2

Đề bài

Cho tam giác ABC cân tại A và nội tiếp đường tròn (O). Tính số đo các góc của tam giác ABC, biết rằng \(\widehat {BOC} = {100^o}\).

Phương pháp giải - Xem chi tiết

Trong một đường tròn, các góc nội tiếp chắn cung nhỏ thì có số đo bằng nửa số đo góc ở tâm chắn cùng một cung.

Lời giải chi tiết

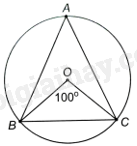
Vì góc nội tiếp BAC và góc ở tâm BOC cùng chắn cung nhỏ BC của (O) nên \(\widehat {BAC} = \frac{1}{2}\widehat {BOC} = {50^o}\).

Vì tam giác ABC cân tại A nên \(\widehat {ABC} = \widehat {ACB} = \frac{1}{2}\left( {{{180}^o} - \widehat {BAC}} \right) = {65^o}\).

Bài trước Bài sau