-
Toán 9 tập 1
-
Toán 9 tập 2
Giải bài tập 3 trang 74 SGK Toán 9 tập 2 - Chân trời sáng tạo
Đề bài
Xác định tâm và bán kính đường tròn ngoại tiếp hình chữ nhật ABCD trong mỗi trường hợp sau:
a) AB = 6 cm, BC = 8 cm;
b) AC = 9cm.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Đọc kĩ dữ liệu để vẽ hình.
- Dựa vào: Đường tròn ngoại tiếp hình chữ nhật, hình vuông có tâm là giao điểm của hai đường chéo và có bán kính bằng nửa đường chéo.
Lời giải chi tiết
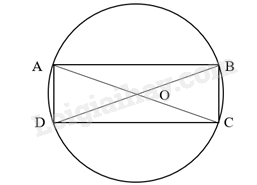
Tâm O của đường tròn ngoại tiếp hình chữ nhật ABCD là giao điểm của hai đường chéo AC và BD, bán kính R = OA = OB = OC = OD = \(\frac{{AC}}{2}\).
a) Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \) (Định lý Pytagore)
\(AC = \sqrt {{6^2} + {8^2}} \) = 10 cm.
Suy ra R = \(\frac{{AC}}{2} = \frac{{10}}{2} = 5\) cm.
b) \(R = \frac{{AC}}{2} = \frac{9}{2} = 4,5\)cm.