-
Toán 9 tập 1
-
Toán 9 tập 2
Giải bài tập 4.9 trang 86 SGK Toán 9 tập 1 - Cùng khám phá
Đề bài
Tính độ dài cạnh bên CD của hình thang ABCD trong Hình 4.24.
Phương pháp giải - Xem chi tiết
+ Kẻ DK vuông góc với BC tại K.
+ Tam giác AHB vuông tại H nên \(AH = AB.\sin B\).
+ Chứng minh tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH\).
+ Áp dụng định lí Pythagore vào tam giác DKC vuông tại K để tính CD.
Lời giải chi tiết
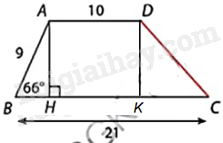
Kẻ DK vuông góc với BC tại K.
\(\Delta \)AHB vuông tại H nên
\(AH = AB.\sin B = 9.\sin {66^o} \approx 8,2\)
\(BH = AB.\cos B = 9.\cos {66^o} \approx 3,7\)
Tứ giác AHKD có: AD//HK (gt), AH//DK (cùng vuông góc với BC) nên tứ giác AHKD là hình bình hành. Do đó, \(HK = AD = 10,DK = AH \approx 8,2\).
Độ dài đoạn thẳng KC là:
\(KC = BC - BH - HK \approx 21 - 3,7 - 10 = 7,3\)
\(\Delta \)DKC vuông tại K nên
\(D{C^2} = D{K^2} + K{C^2} \approx 8,{2^2} + {7,3^2} = 120,53\) (Định lí Pythagore) nên \(DC \approx 11\).