-
Toán 9 tập 1
-
Toán 9 tập 2
Giải bài tập 7 trang 89 SGK Toán 9 tập 1 - Chân trời sáng tạo
Đề bài
Cho đường tròn (O) , điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA và MB (A; B là hai tiếp điểm) thoả mãn \(\widehat {AMB} = {60^o}\). Biết chu vi tam giác MAB là 18 cm, tính độ dài dây AB.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
- Dựa vào dữ kiện đề bài để vẽ hình.
- Chứng minh tam giác AOM = tam giác BMO. Suy ra MA = MB thì tam giác AMB cân tại M
- Chứng minh tam giác AMB đều suy ra độ dài AB từ chu vi tam giác MAB.
Lời giải chi tiết
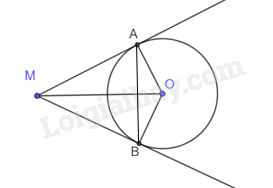
Vì AM, MB là hai tiếp tuyến suy ra \(MA \bot AO;MB \bot BO\).
Xét tam giác vuông AMO và tam giác vuông BMO có:
MO là cạnh chung
OA = OB
Suy ra \(\Delta \)AMO = \(\Delta \)BMO (cạnh huyền – cạnh góc vuông)
Nên MA = MB. Do đó tam giác MAB cân tại M.
Mặt khác, ta có: \(\widehat {AMB} = {60^o}\) nên tam giác MAB đều suy ra AB = MA = MB
Mà AB + AM + MB = \({P_{MAB}}\) = 18
Suy ra 3AB = 18 nên AB = 6 cm.