Giải mục 3 trang 61 SGK Toán 8 – Chân trời sáng tạo
TH 3
Video hướng dẫn giải
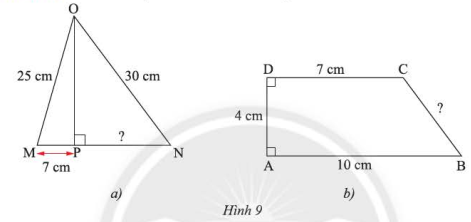
Tính các độ dài \(PN\) và \(BC\) trong Hình 9.
Phương pháp giải:
a. Sử dụng định lý Pythagore tính độ dài đoạn thẳng \(OP\), \(PN\).
b. Kẻ đường cao CH, sử dụng định lý Pythagore tính độ dài đoạn thẳng \(BC\).
Lời giải chi tiết:
a) Áp dụng định lý Pythagore vào tam giác vuông \(OMP\) ta có:
\(O{P^2} + M{P^2} = O{M^2}\)
\(O{P^2} + {7^2} = {25^2}\)
\(O{P^2} + 49 = 625\)
\(O{P^2} = 625 - 49 = 576 = {24^2}\)
\(OP = 24\) (cm)
Áp dụng định lý Pythagore vào tam giác vuông \(OPN\) ta có:
\(P{N^2} + O{P^2} = O{N^2}\)
\(P{N^2} + {24^2} = {30^2}\)
\(P{N^2} = {30^2} - {24^2} = 324 = {18^2}\)
\(PN = 18\) (cm)
b) Kẻ đường cao \(CH\) như trong hình vẽ
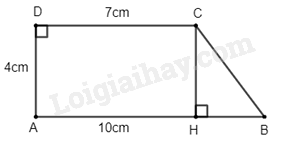
Ta có: \(CH = AD = 4\)cm; \(AH = CD = 7\)cm
\(BH = AB - AH = 10 - 7 = 3\)(cm)
Áp dụng định lý Pythagore vào tam giác vuông \(BCH\) ta có:
\(B{C^2} = C{H^2} + B{H^2}\)
\(B{C^2} = {4^2} + {3^2} = 16 + 9 = 25 = {5^2}\)
\(BC = 5\) (cm)
VD 3
Video hướng dẫn giải
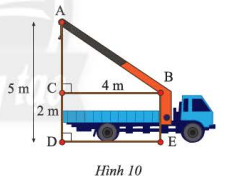
Tính chiều dài cần cẩu \(AB\) trong Hình 10.
Phương pháp giải:
Tính độ dài \(AC\)
Sử dụng định lý Pythagore tính chiều dài cần cẩu
Lời giải chi tiết:
\(AC = AD - CD = 5 - 2 = 3\) (m)
Áp dụng định lý Pythagore vào tam giác vuông \(ABC\) ta có:
\(A{B^2} = A{C^2} + B{C^2}\)
\(A{B^2} = {3^2} + {4^2} = 9 + 16 = 25 = {5^2}\)
\(AB = 5\)(m)
Vậy chiều dài cần cẩu \(AB\) là 5m

