Hình đồng dạng

1. Lý thuyết

- Hình đồng dạng phối cảnh (Hình vị tự).

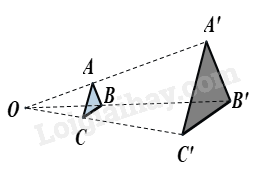
+ Hình ảnh bên từ điểm O, phóng to hai lần tam giác ABC, ta sẽ nhận được tam giác A’B’C’. Hai tam giác A’B’C’ và ABC gọi là đồng dạng phối cảnh (hay vị tự) với nhau, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số \(k = \frac{{A'B'}}{{AB}} = 3\) gọi là tỉ số vị tự.

+ Hình ảnh bên từ điểm O, thu nhỏ hai lần tứ giác ABCD, ta sẽ nhận được tứ giác A’B’C’D’. Hai tứ giác A’B’C’D’ và ABCD gọi là đồng dạng phối cảnh (hay vị tự) với nhau, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số \(k = \frac{{A'B'}}{{AB}} = \frac{1}{2}\) gọi là tỉ số vị tự.

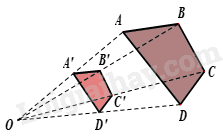
+ Như vậy, bằng cách phóng to (nếu tỉ số vị tự k > 1) hay thu nhỏ (nếu tỉ số vị tự k < 1) hình H, ta sẽ nhận được hình H  ’ đồng dạng phối cảnh (hay vị tự) với hình H.

+ Ta cũng gọi H ’ là hình đồng dạng phối cảnh (hay hình vị tự ) tỉ số k của hình H.

+ Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng AB là một đoạn thẳng A’B’ ( nằm trên đường thẳng song song hoặc trùng với đường thẳng AB) và A’B’ = k.AB.

- Hình đồng dạng.

+ Nếu có thể đặt hình H chồng khít lên hình H ’ thì ta nói hai hình H và H ’ là bằng nhau (hay còn gọi là hình H  bằng hình H ’).

+ Hai hình đồng dạng phối cảnh (hay vị tự) cũng là hai hình đồng dạng.

2. Ví dụ minh họa

 

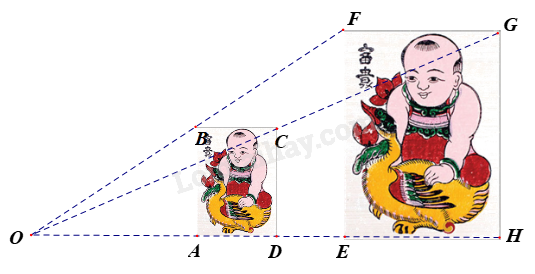
Hình chữ nhật ABCD và EFGH đồng dạng phối cảnh với điểm O gọi là tâm đồng dạng phối cảnh.

Ví dụ về hình đồng dạng: