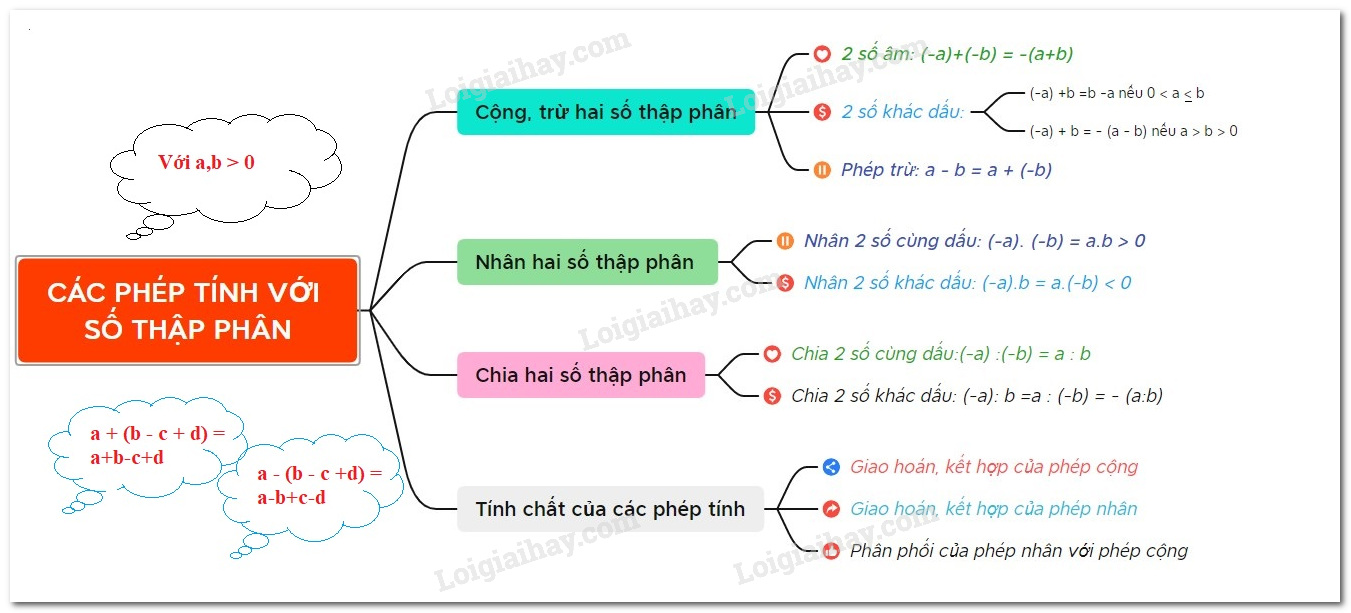
Lý thuyết Các phép tính với số thập phân Toán 6 Chân trời sáng tạo

Cộng hai số thập phân âm:

$ \left( { - a} \right) + \left( { - b} \right) = - \left( {a + b} \right)$ với $ a,\,\,b > 0$

Cộng hai số thập phân khác dấu:

$ \left( { - a} \right) + b = b - a$ nếu $ 0 < a \le b$ ;

$ \left( { - a} \right) + b = - \left( {a - b} \right)$ nếu $ a > b > 0$ .

Phép trừ hai số thập phân được đưa về phép cộng với số đối:

$ a - b = a + \left( { - b} \right)$ .

Ví dụ:

a) $ \left( { - 24,5} \right) + \left( { - 3,16} \right) = - \left( {24,5 + 3,16} \right) = - 27,66$

b) $ 1,5 - 3,169 = 1,5 + \left( { - 3,169} \right) = - \left( {3,169 - 1,5} \right) = - 1,669;$

c) $ 25,689 - \left( { - 1,2345} \right) = 25,689 + 1,2345 = 26,9235$ .

Nhân hai số cùng dấu:

$ \left( { - a} \right).\left( { - b} \right) = a.b$ với $ a,\,\,b > 0$ .

Nhân hai số khác dấu:

$ \left( { - a} \right).b = a.\left( { - b} \right) = - \left( {a.b} \right)$ với $ a,\,b > 0$ .

Ví dụ:

a) Nhân hai số nguyên cùng dấu:

$ \left( { - 1,25} \right).\left( { - 2,41} \right) = 1,25.2,41 = 3,0125$ .

b) Nhân hai số nguyên khác dấu:

$ 2,72.\left( { - 3,25} \right) = - \left( {2,72.3,25} \right) = - 8,84$ .

Chia hai số cùng dấu:

$ \left( { - a} \right):\left( { - b} \right) = a:b$ với $ a,\,\,b > 0$ .

Chia hai số khác dấu:

$ \left( { - a} \right):b = a:\left( { - b} \right) = - \left( {a:b} \right)$ với $ a,\,b > 0$ .

Ví dụ:

a) $ \left( {- 1,45} \right):\left( { - 2,5} \right) = 1,45:2,5 = 0,58$

b) $ \left( { - 5,24} \right):1,31 = - \left( {5,24:1,31} \right) = - 4$

Giống như các phép tính với số nguyên và phân số, các phép tính với số thập phân cũng có đầy đủ các tính chất như:

- Tính chất giao hoán và tính chất kết hợp của phép cộng.

- Tính chất giao hoán và tính chất kết hợp của phép nhân.

- Tính chất phân phối của phép nhân đối với phép cộng.

Vận dụng các tính chất của các phép tính với số thập phân và quy tắc dấu ngoặc, ta có thể tính giá trị các biểu thức một cách hợp lí.

Ví dụ:

$ \begin{array}{l}3,45 - 5,7 + 8,55 = \left( {3,45 + 8,55} \right) - 5,7\\ = 12 - 5,7 = 6,3\end{array}$

Bài trước Bài sau