Lý thuyết Các quy tắc tính đạo hàm - SGK Toán 11 Cùng khám phá

A. Lý thuyết

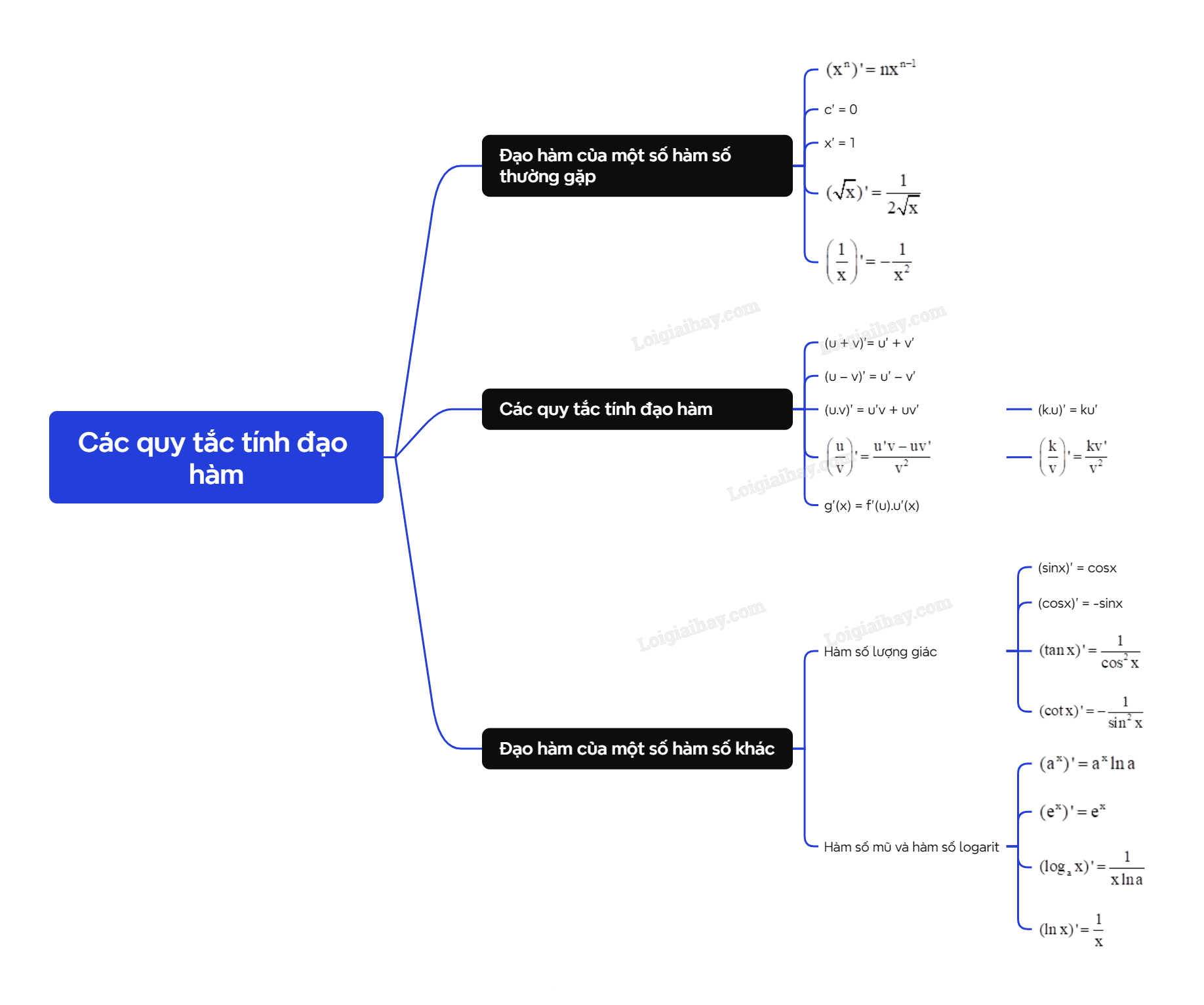
1. Đạo hàm của một số hàm số thường gặp

Hàm số \(y = {x^n}\) \((n \in {\mathbb{N}^*})\) có đạo hàm tại mọi \(x \in \mathbb{R}\) và \(({x^n})' = n{x^{n - 1}}\).

Ghi chú:

+ c’ = 0.

+ x’ = 1.

+ \((\sqrt x )' = \frac{1}{{2\sqrt x }}\) \((x \ne 0)\).

+ \(\left( {\frac{1}{x}} \right)' =  - \frac{1}{{{x^2}}}\) \((x \ne 0)\).

2. Các quy tắc tính đạo hàm

a) Đạo hàm của tổng, hiệu hai hàm số

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm trên khoảng (a;b) thì (u + v)’= u’ + v’; (u – v)’ = u’ – v’.

b) Đạo hàm của tích, thương hai hàm số

Nếu hai hàm số u = u(x) và v = v(x) có đạo hàm trên khoảng xác định thì (u.v)’ = u’v + uv’; \(\left( {\frac{u}{v}} \right)' = \frac{{u'v - uv'}}{{{v^2}}}\) \((v = v(x) \ne 0)\).

Lưu ý:

+ (k.u)’ = ku’ với \(k \in \mathbb{R}\).

+ \(\left( {\frac{k}{v}} \right)' = \frac{{kv'}}{{{v^2}}}\) với \(k \in \mathbb{R}\).

c) Đạo hàm của hàm hợp

* Hàm hợp

Cho hai hàm số f(u) và u = u(x). Hàm số y = f(u(x)) được gọi là hàm số hợp của hai hàm số f(u) và u(x).

* Đạo hàm của hàm hợp

Nếu hàm số u = u(x) có đạo hàm tại x là u’(x) và u = f(u) có đạo hàm tại u là f’(u) thì hàm hợp g(x) = f(u(x)) có đạo hàm tại x là g’(x) = f’(u).u’(x).

3. Đạo hàm của một số hàm số khác

a) Đạo hàm của hàm số lượng giác

+ (sinx)’ = cosx + (cosx)’ = -sinx + \((\tan x)' = \frac{1}{{{{\cos }^2}x}}\), \(x \ne \frac{\pi }{2} + k\pi \) \((k \in \mathbb{Z})\) + \((\cot x)' =  - \frac{1}{{{{\sin }^2}x}}\), \(x \ne k\pi \) \((k \in \mathbb{Z})\)

b) Đạo hàm của hàm số mũ và hàm số logarit

Cho a > 0, \(a \ne 1\). + \(({a^x})' = {a^x}\ln a\) + \(({e^x})' = {e^x}\), \(x \in \mathbb{R}\) + \(({\log _a}x)' = \frac{1}{{x\ln a}}\), x > 0 + \((\ln x)' = \frac{1}{x}\), x > 0

 

B. Bài tập

Bài 1: Tính đạo hàm của hàm số \(y = {x^5} - {x^3} + x - 10\).

Giải:

\(y' = \left( {{x^5}} \right)' - \left( {{x^3}} \right)' + \left( x \right)' - \left( {10} \right)' = 5{x^4} - 3{x^2} + 1\).

Bài 2: Tính đạo hàm của các hàm số sau:

a) \(y = 4{x^2} - \frac{{\sqrt x }}{2} + \frac{5}{x}\).

b) \(y = (2{x^3} + 1)(\sqrt x  - 3)\).

c) \(y = \frac{{2x - 1}}{{x + 1}}\).

Giải:

a) Với x > 0, ta có \(y = 4\left( {{x^2}} \right)' - \frac{1}{2}\left( {\sqrt x } \right)' + 5\left( {\frac{1}{x}} \right)' = 8x - \frac{1}{{4\sqrt x }} - \frac{5}{{{x^2}}}\).

b) Với x > 0, ta có \(y' = (2{x^3} + 1)'(\sqrt x  - 3) + (2{x^3} + 1)(\sqrt x  - 3)' = 6{x^2}(\sqrt x  - 3) + (2{x^3} + 1)\frac{1}{{2\sqrt x }}\).

c) Với \(x \ne  - 1\), ta có \(y' = \frac{{\left( {2x - 1} \right)'\left( {x + 1} \right) - \left( {2x - 1} \right)\left( {x + 1} \right)'}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{2(x + 1) - (2x - 1)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{3}{{{{\left( {x + 1} \right)}^2}}}\).

Bài 3: Tính đạo hàm của các hàm số sau:

a) \(y = {({x^2} + x)^8}\).

b) \(y = \frac{1}{{\sqrt x  + 1}}\).

Giải:

a) \(y = \left[ {{{({x^2} + x)}^8}} \right]' = ({x^2} + x)'.8{({x^2} + x)^{8 - 1}} = 8(2x + 1){({x^2} + x)^7}\).

b) \(y' = \left( {\frac{1}{{\sqrt x  + 1}}} \right)' = \frac{{\left( {\sqrt x  + 1} \right)'}}{{{{\left( {\sqrt x  + 1} \right)}^2}}} = \frac{1}{{{{\left( {\sqrt x  + 1} \right)}^2}}}.\frac{1}{{2\sqrt x }}\).

Bài 4: Tính đạo hàm của các hàm số sau:

a) \(y = 2\sin x - 3\cos x\).

b) \(y = x\tan x\).

c) \(y = \sin \left( {2x - \frac{\pi }{6}} \right)\).

d) \(y = {\cos ^3}3x\).

Giải:

a) \(y' = 2\left( {\sin x} \right)' - 3\left( {\cos x} \right)' = 2\cos x + 3\sin x\).

b) Với \(x \ne \frac{\pi }{2} + k\pi \) \((k \in \mathbb{Z})\), ta có \(y = x'.\tan x + x.(\tan x)' = \tan x + \frac{x}{{{{\cos }^2}x}}\).

c) \(y = \sin \left( {2x - \frac{\pi }{6}} \right)\).

d) \(y' = 3{\cos ^2}3x.(\cos 3x)' =  - 3{\cos ^2}3x.(3x)'.\sin 3x =  - 9{\cos ^2}3x.\sin 3x\).

Bài 5: Tính đạo hàm của các hàm số sau:

a) \(y = {3^{2{x^2} - x}}\).

b) \(y = {\log _2}({x^2} + 2x + 3)\).

c) \(y = x{e^x}\).

Giải:

a) \(y' = (2{x^2} - x)'{.3^{2{x^2} - x}}.\ln 3 = (4x - 1){.3^{2{x^2} - x}}.\ln 3\).

b) \(y' = \frac{{({x^2} + 2x + 3)'}}{{({x^2} + 2x + 3)\ln 2}} = \frac{{2x + 2}}{{({x^2} + 2x + 3)\ln 2}}\).

c) \(y' = (x)'{e^x} + x({e^x})' = {e^x} + x{e^x}\).