- Trang chủ
- Lớp 8
- Toán học Lớp 8
- SGK Toán - Kết nối tri thức Lớp 8
- Toán 8 tập 2
- Chương 9 Tam giác đồng dạng
-
Toán 8 tập 1 với cuộc sống

-
Toán 8 tập 2

Lý thuyết Định lí Pythagore và ứng dụng SGK Toán 8 - Kết nối tri thức
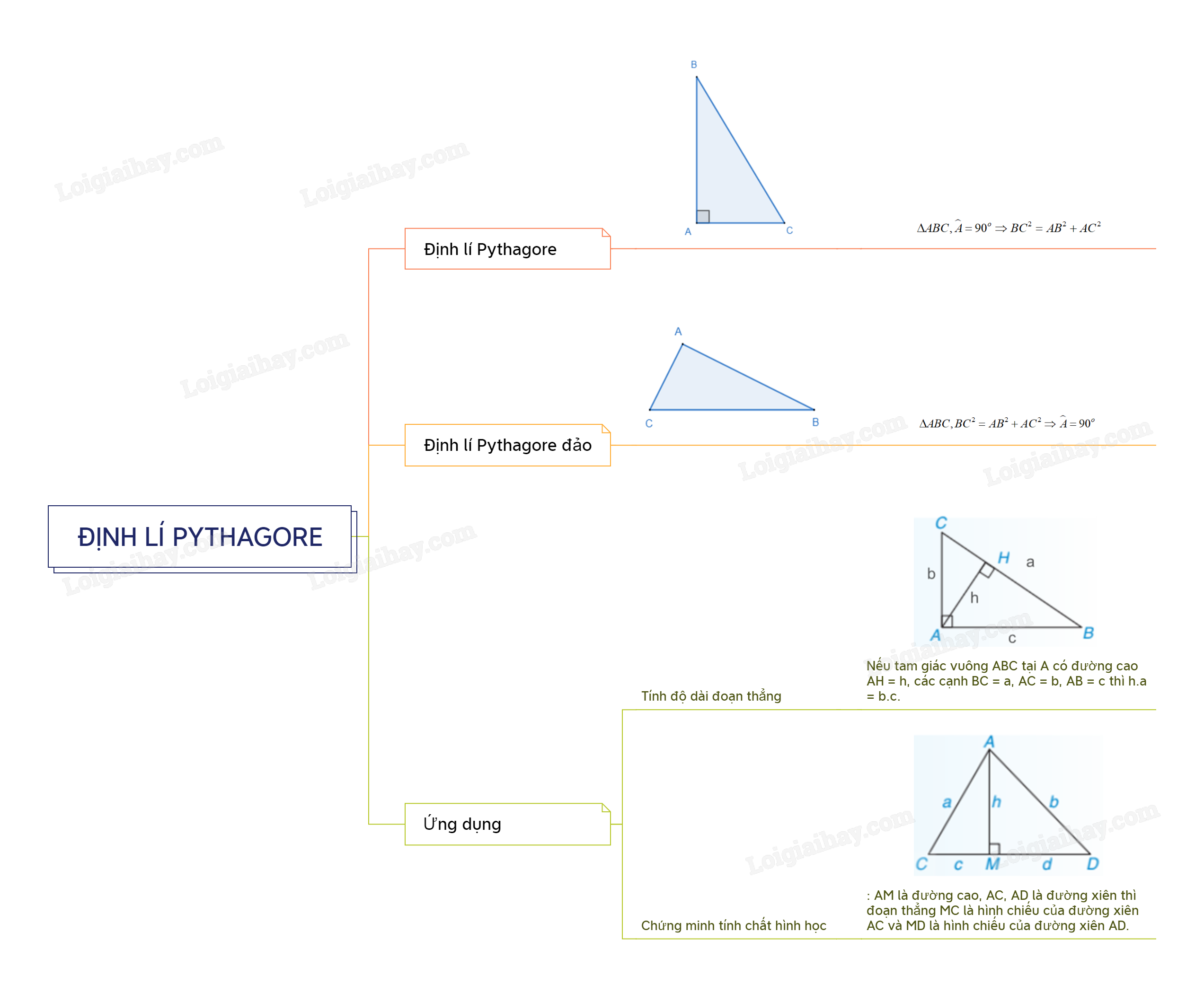
1. Định lí Pythagore
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
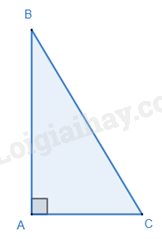
\(\Delta ABC,\widehat A = {90^o} \Rightarrow B{C^2} = A{B^2} + A{C^2}\)
Ví dụ:
Tam giác ABC có AB = 3cm, BC = 5cm, AC = 4cm thì tam giác ABC vuông tại A do \({3^2} + {4^2} = {5^2}\), suy ra \(B{C^2} = A{B^2} + A{C^2}\).
2. Định lí Pythagore đảo
Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
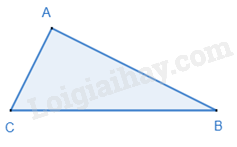
\(\Delta ABC,B{C^2} = A{B^2} + A{C^2} \Rightarrow \widehat A = {90^o}\)
3. Ứng dụng của định lí Pythagore
a. Tính độ dài đoạn thẳng
Nhận xét: Nếu tam giác vuông ABC tại A có đường cao AH = h, các cạnh BC = a, AC = b, AB = c thì h.a = b.c.
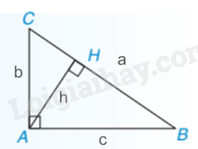
Ví dụ: Tam giác ABC vuông tại A có AB = 5cm, AC = 12cm thì BC = \(\sqrt {{5^2} + {{12}^2}} = \sqrt {169} = 13\)
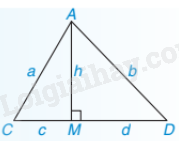
b. Chứng minh tính chất hình học
Chú ý: AM là đường cao, AC, AD là đường xiên thì đoạn thẳng MC là hình chiếu của đường xiên AC và MD là hình chiếu của đường xiên AD.
- Giải mục 1 trang 93, 94, 95 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải mục 2 trang 95, 96, 97 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 9.17 trang 97 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 9.18 trang 97 SGK Toán 8 tập 2 - Kết nối tri thức
- Giải bài 9.19 trang 97 SGK Toán 8 tập 2 - Kết nối tri thức
