- Trang chủ
- Lớp 6
- Toán học Lớp 6
- SGK Toán Lớp 6 Cánh diều
- Toán 6 tập 1 Cánh diều
- CHƯƠNG 3. HÌNH HỌC TRỰC QUAN
-
Toán 6 tập 1

-
 CHƯƠNG 1.SỐ TỰ NHIÊN
CHƯƠNG 1.SỐ TỰ NHIÊN
- Bài 1. Tập hợp
- Bài 2. Tập hợp các số tự nhiên
- Bài 3. Phép cộng, phép trừ các số tự nhiên
- Bài 4. Phép nhân, phép chia với các số tự nhiên
- Bài 5. Phép tính lũy thừa với số mũ tự nhiên
- Bài 6. Thứ tự thực hiện các phép tính
- Bài 7. Quan hệ chia hết. Tính chất chia hết
- Bài 8. Dấu hiệu chia hết cho 2, cho 5
- Bài 9. Dấu hiệu chia hết cho 3, cho 9
- Bài 10. Số nguyên tố. Hợp số
- Bài 11. Phân tích một số ra thừa số nguyên tố
- Bài 12. Ước chung và ước chung lớn nhất
- Bài 13. Bội chung và bội chung nhỏ nhất
- Bài tập cuối chương 1
-
 CHƯƠNG 2.SỐ NGUYÊN
CHƯƠNG 2.SỐ NGUYÊN
-
 CHƯƠNG 3. HÌNH HỌC TRỰC QUAN
CHƯƠNG 3. HÌNH HỌC TRỰC QUAN
-
-
Toán 6 tập 2

-
 CHƯƠNG 4. MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT
CHƯƠNG 4. MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT
-
 CHƯƠNG 5. PHÂN SỐ VÀ SỐ THẬP PHÂN
CHƯƠNG 5. PHÂN SỐ VÀ SỐ THẬP PHÂN
- Bài 1. Phân số với tử và mẫu là số nguyên
- Bài 2. So sánh các phân số. Hỗn số dương
- Bài 3. Phép cộng và phép trừ phân số
- Bài 4. Phép nhân và phép chia phân số
- Bài 5. Số thập phân
- Bài 6. Phép cộng và phép trừ số thập phân
- Bài 7. Phép nhân, phép chia số thập phân
- Bài 8. Ước lượng và làm tròn số
- Bài 9. Tỉ số. Tỉ số phần trăm
- Bài 10. Hai bài toán về phân số
- Bài tập cuối chương 5
- Hoạt động thực hành và trải nghiệm chủ đề 2
-
 CHƯƠNG 6. HÌNH HỌC PHẲNG
CHƯƠNG 6. HÌNH HỌC PHẲNG
-
Lý thuyết Đối xứng trong thực tiễn Toán 6 Cánh diều
I. Tính đối xứng trong tự nhiên
Tính đối xứng có vai trò quan trọng trong tự nhiên:
- Tính đối xứng của một đối tượng là một trong những dấu hiệu quan trọng nhất giúp chúng ta nhanh chóng định hình đối tượng khi nhìn vào nó.
- Tính đối xứng thường xuất hiện trong thế giới động vật và thực vật, giúp chúng cân bằng vững chắc, hài hoà và nhờ đó tạo ra thẩm mĩ đẹp.
Ví dụ:
Một số hình ảnh đối xứng trong tự nhiên
II. Tính đối xứng trong khoa học, kĩ thuật và đời sống
- Bố cục đối xứng đem lại cho các công trình, máy móc tính ổn định, bền vững và có được vẻ đẹp, bắt mắt.
- Trong công nghệ chế tạo tính đối xứng được sử dụng nhiều trong công nghệ chế tạo giúp các vật có tính cần bằng, hài hoà, vững chắc.
Trong hội hoạ, kiến trúc, xây dựng: Tính đối xứng thể hiện rõ nét trong hội hoạ và kiến trúc, nó đem lại cảm hứng cho các hoạ sĩ và kiến trúc sư.
Ví dụ:
a.Tính đối xứng trong xây dựng, kiến trúc
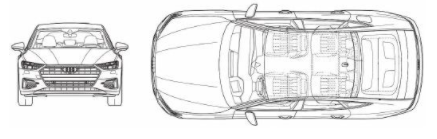
b.Tính đối xứng trong công nghệ