Lý thuyết Hình chóp tam giác đều SGK Toán 8 - Cánh diều

1. Khái niệm 

 

Hình chóp tam giác đều có 4 mặt, 6 cạnh:

- Đáy là tam giác đều.

- 3 cạnh bên bằng nhau.

- 3 mặt bên là các tam giác cân bằng nhau và có chung một đỉnh.

- 3 cạnh đáy bằng nhau là ba cạnh của tam giác đáy.

- Chân đường cao trùng với tâm của đáy.

2. Công thức tính diện tích xung quanh của hình chóp tam giác đều

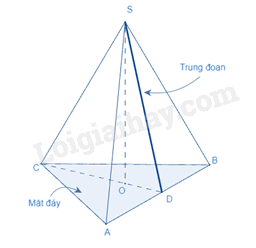
Diện tích xung quanh của hình chóp tam giác đều bằng nửa chu vi đáy với độ dài trung đoạn.

\(Sxq = p.d\) 

(là diện tích xung quanh, p là nửa chu vi đáy, d là trung đoạn)

Công thức tính thể tích của hình chóp tam giác đều

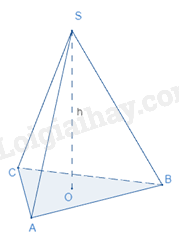
Thể tích của hình chóp tam giác đều bằng diện tích đáy nhân với chiều cao.

\(V = \frac{1}{3}.h.S­_{đáy}\)

(V là thể tích, \(S­_{đáy}\) là diện tích đáy, h là chiều cao)

Ví dụ: 

Cho hình chóp tam giác đều sau:

 

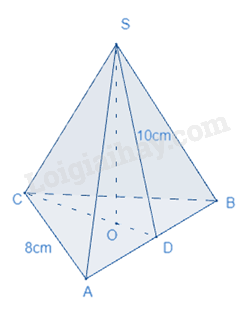
Diện tích xung quanh của hình chóp là:

\({S_{xq}} = \frac{{3.8}}{2}.10 = 120(c{m^2})\)

Cho hình chóp tam giác đều sau:

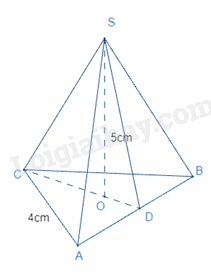
Chiều cao của mặt đáy là:

\(CD = \sqrt {{4^2} - {{\left( {\frac{4}{2}} \right)}^2}}  = 2\sqrt 3 (cm)\)

Thể tích của hình chóp là:

\(V = \frac{1}{3}.5.\frac{{4.2\sqrt 3 }}{2} = \frac{{20\sqrt 3 }}{3}(c{m^3})\)