1. Trang chủ
  2. Lớp 6
  3. Toán học Lớp 6
  4. SGK Toán Lớp 6 Chân trời sáng tạo
  5. GIẢI TOÁN 6 SỐ VÀ ĐẠI SỐ TẬP 2 CHÂN TRỜI SÁNG TẠO Chân trời sáng tạo
  6. CHƯƠNG 6. SỐ THẬP PHÂN

Lý thuyết Làm tròn số thập phân và ước lượng kết quả Toán 6 Chân trời sáng tạo

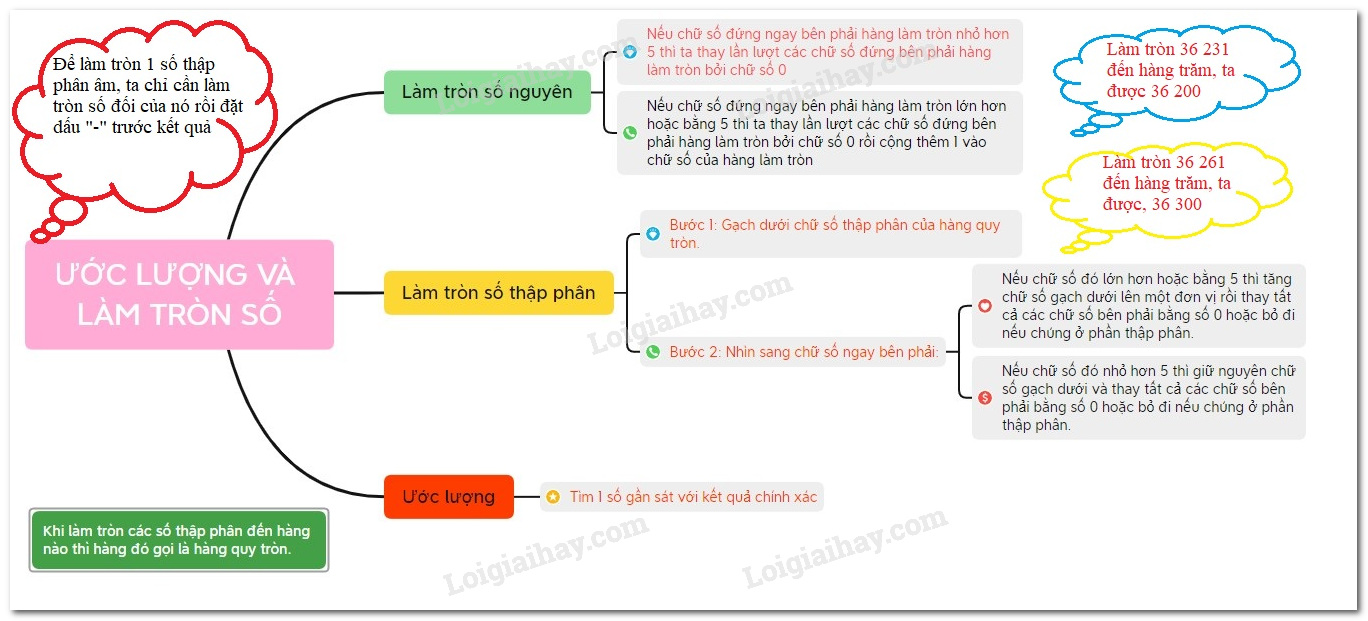
I. Làm tròn số nguyên

Để làm tròn một số nguyên (có nhiều chữ số) đến một hàng nào đó, ta làm như sau:

- Nếu chữ số đứng ngay bên phải hàng làm tròn nhỏ hơn $5$ thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số $0$.

- Nếu chữ số đứng ngay bên phải hàng làm tròn lớn hơn hoặc bằng 5 thì ta thay lần lượt các chữ số đứng bên phải hàng làm tròn bởi chữ số $0$ rồi cộng thêm $1$ vào chữ số của hàng làm tròn.

Chú ý: Kí hiệu “ ” đọc là “gần bằng” hoặc “xấp xỉ”.

Ví dụ:

Làm tròn số $125\,\,356$ đến hàng nghìn

Do chữ số hàng trăm là $3$ nên: $125\,\,356 \approx 125\,\,000$

II. Làm tròn số thập phân

Để làm tròn một số thập phân dương đến một hàng nào đấy (gọi là hàng làm tròn), ta làm như sau:

- Đối với chữ số hàng làm tròn:

  • Giữ nguyên nếu chữ số ngay bên phải nhỏ hơn $5$;
  • Tăng 1 đơn vị nếu chữ số ngay bên phải lớn hơn hay bằng $5$.

- Đối với các chữ số sau hàng làm tròn:

  • Bỏ đi nếu ở phần thập phân,
  • Thay bởi các chữ số $0$ nếu ở phần số nguyên.

Ví dụ:

Làm tròn số $24,037$ đến hàng phần mười (đến chữ số thập phân thứ nhất).

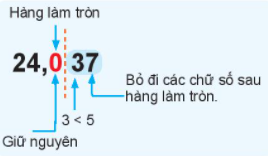
1631932241226_mceclip0.png

Làm tròn số  đến hàng phần mười ta được kết quả là $24,0$

Vậy: $24,037 \approx 24,0$.

III. Ước lượng kết quả

Ta có thể sử dụng quy ước làm tròn số để ước lượng kết quả các phép tính. Nhờ đó có thể dễ dàng phát hiện ra những đáp số không hợp lí.

Ví dụ:

Ước lượng kết quả các phép tính sau:

a) $\left( { - 11,032} \right).\left( { - 24,3} \right) \approx 11.24 = 264$

b) $81.49 \approx 80.50 = 4\,000$

so-do-bai-30_2.jpg

Bài trước Bài sau