- Trang chủ
- Lớp 6
- Toán học Lớp 6
- SGK Toán Lớp 6 Cánh diều
- Toán 6 tập 2 Cánh diều
- CHƯƠNG 5. PHÂN SỐ VÀ SỐ THẬP PHÂN
-
Toán 6 tập 1

-
 CHƯƠNG 1.SỐ TỰ NHIÊN
CHƯƠNG 1.SỐ TỰ NHIÊN
- Bài 1. Tập hợp
- Bài 2. Tập hợp các số tự nhiên
- Bài 3. Phép cộng, phép trừ các số tự nhiên
- Bài 4. Phép nhân, phép chia với các số tự nhiên
- Bài 5. Phép tính lũy thừa với số mũ tự nhiên
- Bài 6. Thứ tự thực hiện các phép tính
- Bài 7. Quan hệ chia hết. Tính chất chia hết
- Bài 8. Dấu hiệu chia hết cho 2, cho 5
- Bài 9. Dấu hiệu chia hết cho 3, cho 9
- Bài 10. Số nguyên tố. Hợp số
- Bài 11. Phân tích một số ra thừa số nguyên tố
- Bài 12. Ước chung và ước chung lớn nhất
- Bài 13. Bội chung và bội chung nhỏ nhất
- Bài tập cuối chương 1
-
 CHƯƠNG 2.SỐ NGUYÊN
CHƯƠNG 2.SỐ NGUYÊN
-
 CHƯƠNG 3. HÌNH HỌC TRỰC QUAN
CHƯƠNG 3. HÌNH HỌC TRỰC QUAN
-
-
Toán 6 tập 2

-
 CHƯƠNG 4. MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT
CHƯƠNG 4. MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT
-
 CHƯƠNG 5. PHÂN SỐ VÀ SỐ THẬP PHÂN
CHƯƠNG 5. PHÂN SỐ VÀ SỐ THẬP PHÂN
- Bài 1. Phân số với tử và mẫu là số nguyên
- Bài 2. So sánh các phân số. Hỗn số dương
- Bài 3. Phép cộng và phép trừ phân số
- Bài 4. Phép nhân và phép chia phân số
- Bài 5. Số thập phân
- Bài 6. Phép cộng và phép trừ số thập phân
- Bài 7. Phép nhân, phép chia số thập phân
- Bài 8. Ước lượng và làm tròn số
- Bài 9. Tỉ số. Tỉ số phần trăm
- Bài 10. Hai bài toán về phân số
- Bài tập cuối chương 5
- Hoạt động thực hành và trải nghiệm chủ đề 2
-
 CHƯƠNG 6. HÌNH HỌC PHẲNG
CHƯƠNG 6. HÌNH HỌC PHẲNG
-
Lý thuyết Phân số với tử và mẫu là số nguyên Toán 6 Cánh diều
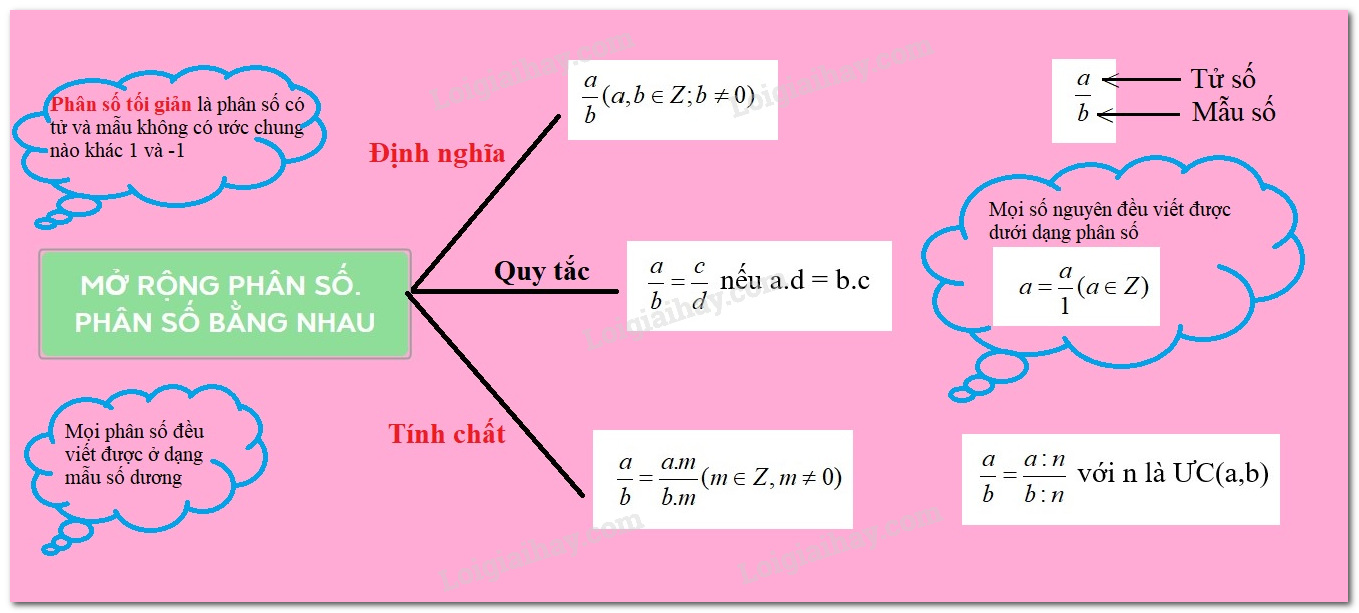
1. Khái niệm phân số
Ta gọi \(\frac{a}{b}\), trong đó \(a,\;b \in \mathbb{Z},\;b \ne 0\)là phân số, a là tử số (tử) và b là mẫu số (mẫu) của phân số. Phân số \(\frac{a}{b}\) đọc là a phần b.
2. Phân số bằng nhau
Hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\) được gọi là bằng nhau, viết là \(\frac{a}{b} = \frac{c}{d}\), nếu \(a.d = b.c\).
Chú ý: Điều kiện \(a.d = b.c\) gọi là điều kiện bằng nhau của hai phân số \(\frac{a}{b}\) và \(\frac{c}{d}\).
3. Tính chất cơ bản của phân số
*Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
*Nếu ta chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
Phương pháp rút gọn về phân số tối giản
Bước 1: Tìm ƯCLN của tử và mẫu sau khi đã bỏ dấu – (nếu có)
Bước 2: Chia cả tử và mẫu cho ước chung lớn nhất vừa tìm được, ta có phân số tối giản cần tìm
Để quy đồng nhiều phân số, ta thường làm như sau:
Bước 1: Viết các phân số đã cho dưới dạng phân số có mẫu dương. Tìm BCNN của các mẫu dương đó để làm mẫu số chung
Bước 2: Tìm thừa số phụ của mỗi mẫu, bằng cách chia mẫu chung cho từng mẫu
Bước 3: Nhân tử và mẫu của mỗi phân số ở Bước 1 với thừa số phụ tương ứng
Chú ý:
Mỗi số nguyên n có thể coi là phân số \(\frac{n}{1}\)(viết \(\frac{n}{1} = n\)). Khi đó số nguyên n được biểu diễm ở dạng phân số \(\frac{n}{1}.\)
Lời giải hay
- Trả lời Câu hỏi khởi động trang 25 SGK Toán 6 Cánh Diều
- Trả lời Hoạt động 1 trang 25 SGK Toán 6 Cánh Diều
- Trả lời Hoạt động 2 trang 25 SGK Toán 6 Cánh Diều
- Trả lời Luyện tập vận dụng 1 trang 26 SGK Toán 6 Cánh Diều tập 2
- Trả lời Luyện tập vận dụng 2 trang 26 SGK Toán 6 Cánh Diều tập 2