-
Toán 8 tập 1

-
Toán 8 tập 2

-
 Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
-
 Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
- Bài 1. Định lí Thalès
- Bài 2. Đường trung bình của tam giác
- Bài 3. Tính chất đường phân giác trong của tam giác
- Bài 4. Tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng cạnh - cạnh - cạnh
- Bài 6. Trường hợp đồng dạng cạnh - góc - cạnh
- Bài 7. Trường hợp đồng dạng góc - góc
- Bài 8. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 9. Hình đồng dạng
- Ôn tập chương 6
-
 Chương 7 Một số yếu tố thống kê và xác suất
Chương 7 Một số yếu tố thống kê và xác suất
-
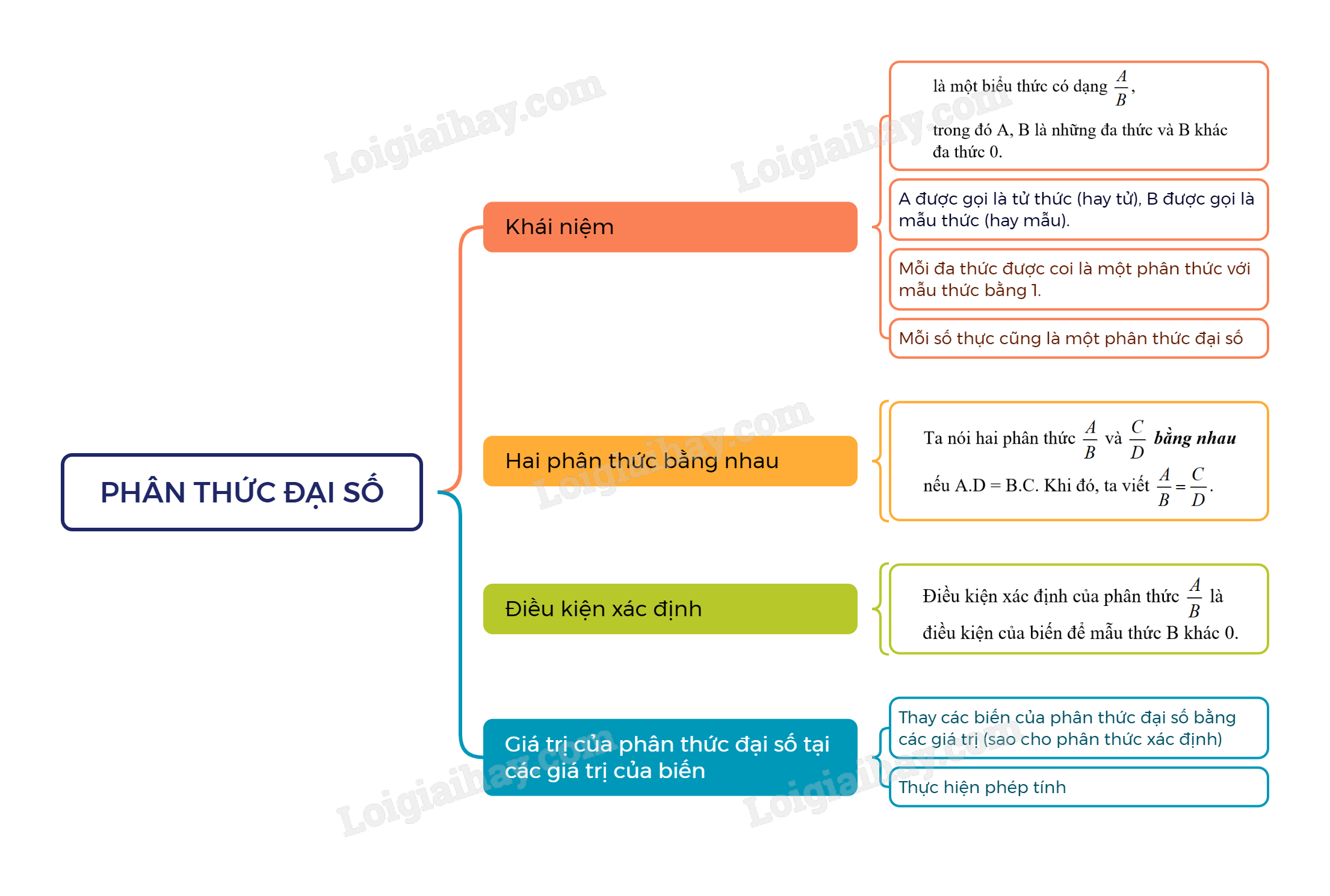
Lý thuyết Phân thức đại số SGK Toán 8 - Cùng khám phá
1. Khái niệm phân thức đại số
Một phân thức đại số (hay còn gọi là phân thức) là một biểu thức có dạng \(\frac{A}{B}\), trong đó A, B là những đa thức và B khác đa thức 0.
A được gọi là tử thức (hay tử), B được gọi là mẫu thức (hay mẫu).
Chú ý: Mỗi đa thức được coi là một phân thức với mẫu thức bằng 1.
Ví dụ: \(\frac{{2x + 1}}{{x - 3}};\frac{{ab}}{{a + b}};{x^2} + 3x + 2;\sqrt 2 \) là các phân thức đại số.
\(\sqrt x ;\sqrt[3]{x}\) không phải là phân thức vì \(\sqrt x ;\sqrt[3]{x}\) không phải là đa thức.
2. Hai phân thức bằng nhau
Hai phân thức \(\frac{A}{B}\) và \(\frac{C}{D}\) bằng nhau, kí hiệu là \(\frac{A}{B} = \frac{C}{D}\) nếu A.D = B.C.
Ví dụ: Hai phân thức \(\frac{{x{y^2}}}{{xy + y}}\) và \(\frac{{xy}}{{x + 1}}\) bằng nhau.
3. Điều kiện xác định của phân thức \(\frac{A}{B}\)
Điều kiện xác định của phân thức \(\frac{A}{B}\) là điều kiện của biến để mẫu thức B khác 0.
Để tính giá trị của phân thức tại giá trị cho trước của các biến (thỏa mãn điều kiện xác định của phân thức), ta thay giá trị các biến vào phân thức rồi thực hiện các phép tính.
Ví dụ: Phân thức P = \(\frac{{x + 3}}{{x - 1}}\) xác định khi \(x - 1 \ne 0\) hay \(x \ne 1\)
Tại x = 3, \(P = \frac{{3 + 3}}{{3 - 1}} = \frac{6}{2} = 3\)