Lý thuyết Thể tích của hình chóp tam giác đều - hình chóp tứ giác đều SGK Toán 8 - Cùng khám phá

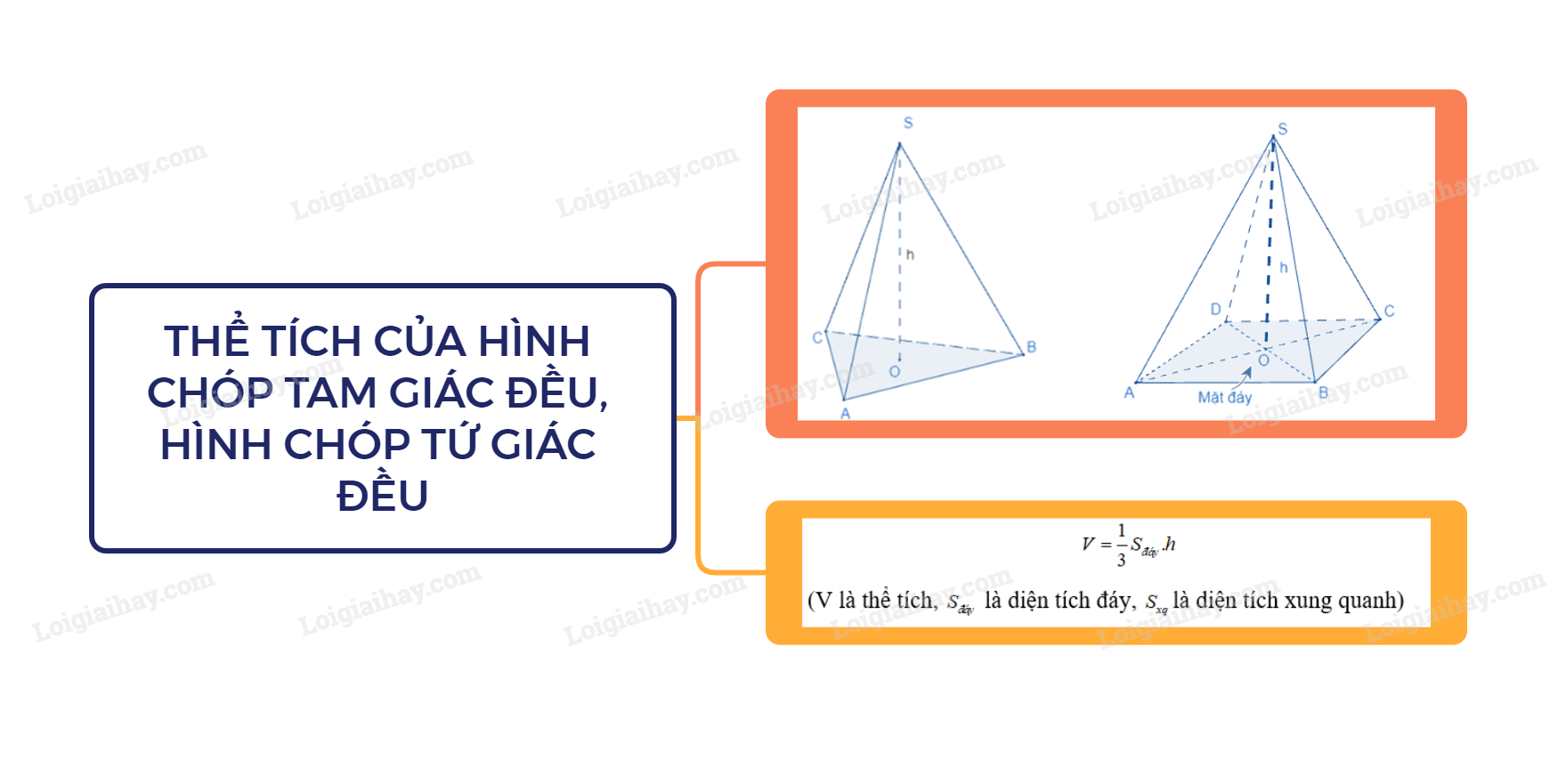
Công thức tính thể tích của hình chóp tam giác đều và hình chóp tứ giác đều

Thể tích của hình chóp tam giác đều (hình chóp tứ giác đều) bằng \(\frac{1}{3}\) diện tích đáy nhân với chiều cao.

\(V = \frac{1}{3}{S_{đáy}}.h\)

(V là thể tích, \({S_{đáy}}\) là diện tích đáy, \({S_{xq}}\) là diện tích xung quanh)

Ví dụ:

Cho hình chóp tứ giác đều sau:

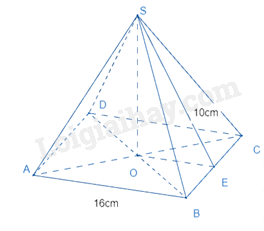
Chiều cao của hình chóp là: \(\sqrt {{{10}^2} - {{\left( {\frac{{16}}{2}} \right)}^2}} = \sqrt {100 - 64} = \sqrt {36} = 6(cm)\)

Thể tích của hình chóp là: \(V = \frac{1}{3}.6.16.16 = 512(c{m^3})\)

c4-b3-the-tich-cua-hinh-chop-tam-giac-deu-hinh-chop-tu-giac-deu.png

Bài trước Bài sau