Tính chất tỉ lệ thức

+ Tính chất 1 (tính chất cơ bản của tỉ lệ thức)

Nếu \(\dfrac{a}{b} = \dfrac{c}{d}\) thì \(a.d = b.c\)

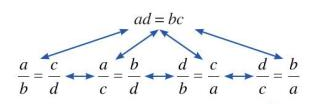
+ Tính chất 2 (điều kiện để bốn số lập thành tỉ lệ thức): Nếu \(ad = bc\) và \(a,b,c,d \ne 0\) thì ta có các tỉ lệ thức

\(\dfrac{a}{b} = \dfrac{c}{d}\); \(\dfrac{a}{c} = \dfrac{b}{d}\); \(\dfrac{d}{b} = \dfrac{c}{a};\) \(\dfrac{d}{c} = \dfrac{b}{a}.\)

Ví dụ: Ta có \(\dfrac{3}{6} = \dfrac{9}{{18}} \Rightarrow 3.18 = 9.6\left( { = 54} \right)\)

Vì \(4.9 = 3.12( = 36)\) nên ta có các tỉ lệ thức sau: \(\dfrac{4}{3} = \dfrac{{12}}{9};{\mkern 1mu} \dfrac{3}{4} = \dfrac{9}{{12}};\dfrac{4}{{12}} = \dfrac{3}{9};\dfrac{{12}}{4} = \dfrac{9}{3}\)