Tứ giác lồi

1. Lý thuyết

Khái niệm:

+ Tứ giác là hình gồm bốn đoạn thẳng, trong đó không có hai đoạn thẳng nào cùng nằm trên một đường thẳng.

+ Tứ giác lồi là tứ giác mà hai đỉnh thuộc một cạnh bất kì luôn nằm về một phía của đường thẳng đi qua hai đỉnh còn lại.

2. Ví dụ minh họa

- Ví dụ: Trong các hình dưới đây, hình 1 được gọi là tứ giác lồi.

 

- Chú ý: Dạng bài toán thường gặp: Bài toán liên quan đến cạnh và đường chéo của tứ giác lồi

Phương pháp giải:

Ta có thể chia tứ giác thành các tam giác, sau đó vận dụng bất đẳng thức tam giác.

Ví dụ: Cho tam giác ABCD. Chứng minh \(AC + BD > \frac{p}{2}\) (p là chu vi tứ giác).

Lời giải:

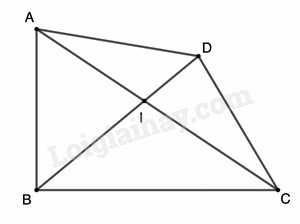
Gọi I là giao điểm của AC và BD. Theo bất đẳng thức tam giác ta có:

\(IA + IB > AB\);

\(IB + IC > BC\);

\(IC + ID > CD\);

\(ID + IA > AD\).

Cộng từng vế, ta được:

\(IA + IB + IB + IC + IC + ID + ID + IA > AB + BC + CD + DA\)

\(2(IA + IB + IC + ID) > AB + BC + CD + DA\)

\(2[(IA + IB) + (IC + ID)] > p\)

\(2(AC + BD) > p\)

\(AC + BD > \frac{p}{2}\) (đpcm)