Bài 7.43 trang 65 SGK Toán 11 tập 2 - Kết nối tri thức
Đề bài
Cho hình lăng trụ \(ABCD.A'B'C'D'\). Biết \(A'.ABCD\) là hình chóp đều có tất cả các cạnh đều bằng nhau và bằng \(a\). Tính theo \(a\) thể tích của khối lăng trụ \(ABCD.A'B'C'D'\) và thể tích của khối chóp \(A'.BB'C'C\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Thể tích khối lăng trụ \(V = h.S\)
Lời giải chi tiết
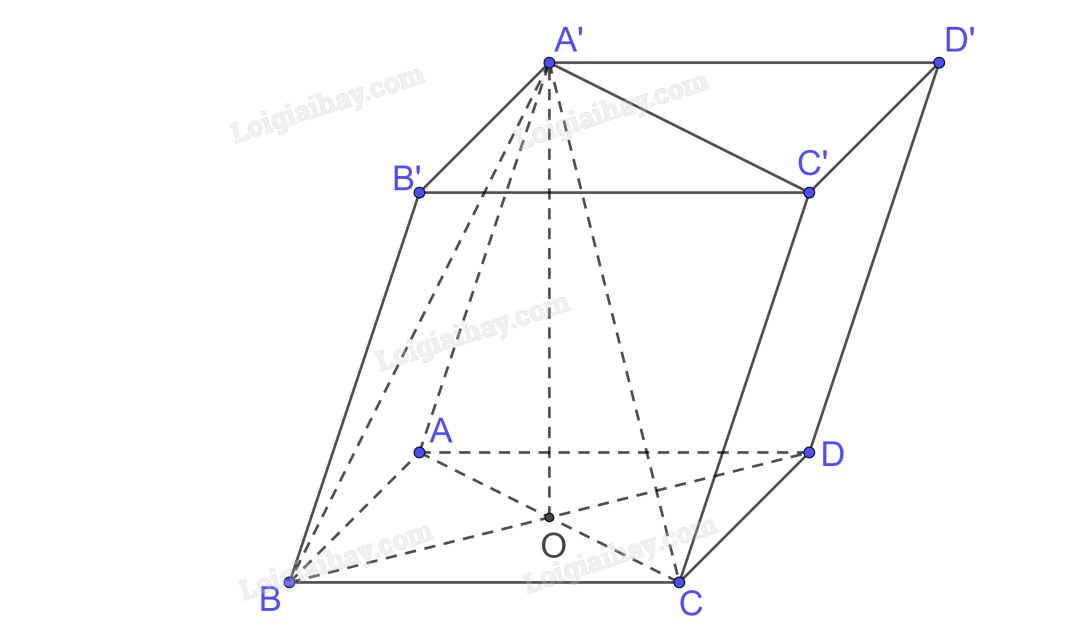
Gọi \(AC \cap BD = \left\{ O \right\}\) mà A’.ABCD là hình chóp đều nên \(A'O \bot \left( {ABCD} \right)\)
Xét tam giác ABC vuông tại B có \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
\( \Rightarrow OA = \frac{{AC}}{2} = \frac{{a\sqrt 2 }}{2}\)
Xét tam giác A’AO vuông tại O có
\(A'O = \sqrt {A{{A'}^2} - A{O^2}} = \sqrt {{a^2} - {{\left( {\frac{{a\sqrt 2 }}{2}} \right)}^2}} = \frac{{a\sqrt 2 }}{2}\)
\({S_{ABCD}} = {a^2}\)
Vậy khối chóp có thể tích \(V_{chóp} = \frac{1}{3}A'O.{S_{ABCD}} = \frac{1}{3}.\frac{{a\sqrt 2 }}{2}.{a^2} = \frac{{{a^3}\sqrt 2 }}{6}.\)
Nếu hình lăng trụ \(ABCD.A'B'C'D'\) xoay lại thành hình lăng trụ AA’D’D.BB’C’C thì thể tích không thay đổi do đó thể tích hình chóp \(A'.BB'C'C\) bằng 1/3 thể tích hình lăng trụ AA’D’D.BB’C’C vì chung đáy và chung chiều cao kẻ từ A’ xuống đáy BB’C’C.
Thể tích khối lăng trụ là \({V_{lăng trụ}} = 3.\frac{{{a^3}\sqrt 2 }}{6} = \frac{{{a^3}\sqrt 2 }}{{2}}.\)

