Giải bài 1 trang 36 sách bài tập toán 12 - Chân trời sáng tạo

Đề bài

Giá thành của một sản phẩm trong 6 tháng đầu năm thay đổi theo công thức \(P\left( t \right) = 2{t^3} - 33{t^2} + 168t + 137\) với \(P\) tính bằng nghìn đồng và \(t\) là số tháng tính từ đầu năm. Trong khoảng thời gian nào thì giá của sản phẩm tăng?

Lời giải chi tiết

Xét hàm số \(P\left( t \right) = 2{t^3} - 33{t^2} + 168t + 137\) trên đoạn \(\left[ {0;6} \right]\).

Ta có: \(P'\left( t \right) = 6{t^2} - 66t + 168;P'\left( t \right) = 0 \Leftrightarrow t = 4\) hoặc \(t = 7\) (loại).

Bảng biến thiên:

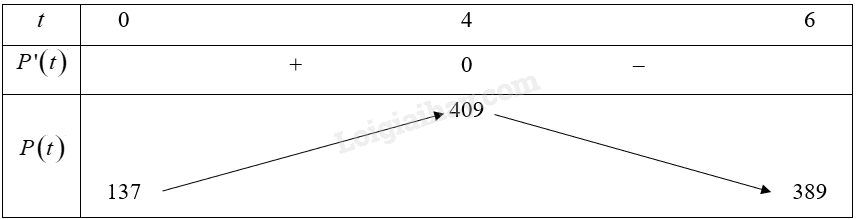
Vậy hàm số đồng biến trên khoảng \(\left( {0;4} \right)\).

Vậy trong khoảng thời gian 4 tháng đầu năm thì giá của sản phẩm tăng.