Giải bài 2 trang 79 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Đề bài
Cho tam giác ABC có đường cao AH (H\( \in \)BC) và nội tiếp đường tròn (O). Vẽ đường kính AD của đường tròn (O). Chứng minh AB.AC = AH.AD
Phương pháp giải - Xem chi tiết
Chứng minh \(\Delta \)AHB và \(\Delta \)ACD đồng dạng với nhau rồi suy ra tỉ số đồng dạng.
Lời giải chi tiết
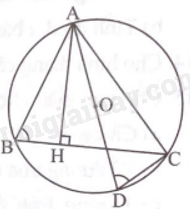
Ta có \(\widehat {ACD}\) là góc nội tiếp chắn nửa đường tròn (O) nên \(\widehat {ACD} = {90^o}\).
Xét \(\Delta \)AHB và \(\Delta \)ACD có \(\widehat {AHB} = \widehat {ACD} = {90^o}\)
\(\widehat {ABH} = \widehat {ADC}\) (hai góc nội tiếp cùng chắn cung AC).
Do đó \(\Delta \)AHB \(\backsim \) \(\Delta \)ACD (g.g).
Suy ra \(\frac{{AB}}{{AD}} = \frac{{AH}}{{AC}}\) hay AB.AC = AH. AD.

