-
Toán 8 tập 1

-
Toán 8 tập 2

-
 Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
Chương 5 Hàm số và đồ thị. Phương trình bậc nhất
-
 Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
Chương 6 Định lí Thalès trong tam giác. Hình đồng dạng
- Bài 1. Định lí Thalès
- Bài 2. Đường trung bình của tam giác
- Bài 3. Tính chất đường phân giác trong của tam giác
- Bài 4. Tam giác đồng dạng
- Bài 5. Trường hợp đồng dạng cạnh - cạnh - cạnh
- Bài 6. Trường hợp đồng dạng cạnh - góc - cạnh
- Bài 7. Trường hợp đồng dạng góc - góc
- Bài 8. Các trường hợp đồng dạng của hai tam giác vuông
- Bài 9. Hình đồng dạng
- Ôn tập chương 6
-
 Chương 7 Một số yếu tố thống kê và xác suất
Chương 7 Một số yếu tố thống kê và xác suất
-
Giải bài 3.2 trang 58 SGK Toán 8 - Cùng khám phá
Đề bài
Tính độ dài đường cao của một tam giác đều có độ dài cạnh bằng \(4cm.\)
Phương pháp giải - Xem chi tiết
Đường cao trong tam giác đều cũng đồng thời là đường trung tuyến.
Sử dụng định lí Pythagore để tính độ dài đường cao đó.
Lời giải chi tiết
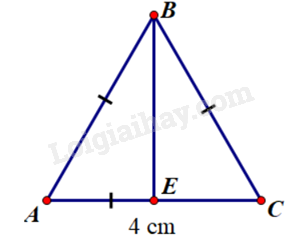
Cho tam giác ABC đều có độ dài cạnh bằng \(4\,cm.\) Kẻ \(BE \bot AC\)
BE vừa là đường cao đồng thời là đường trung tuyến của tam giác ABC.
Suy ra E là trung điểm của AC \( \Rightarrow AE = EC = 2cm\)
Xét tam giác ABE vuông tại E có
\(A{E^2} + B{E^2} = A{B^2}\)(Pythagore)
\(\begin{array}{l} \Rightarrow {2^2} + B{E^2} = {4^2} \Rightarrow B{E^2} = 16 - 4 = 12\\ \Rightarrow BE = 2\sqrt 3 \left( {cm} \right)\end{array}\)
Vậy độ dài đường cao của một tam giác đều có độ dài cạnh bằng \(4cm\) là \(2\sqrt 3 cm\)