- Trang chủ
- Lớp 9
- Toán học Lớp 9
- SBT Toán Lớp 9 Chân trời sáng tạo
- SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO Chân trời sáng tạo
- Chương 4. Hệ thức lượng trong tam giác vuông
-
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO

-
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO

Giải bài 4 trang 72 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Đề bài
Từ chân một tháp cao 50 m người ta nhìn thấy đỉnh của một toà nhà với góc nâng 30o. Trong khi đó từ chân toà nhà, người ta lại nhìn thấy đỉnh tháp với góc nâng 60o. Tính chiều cao của toà nhà.

Phương pháp giải - Xem chi tiết
Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng.
Lời giải chi tiết
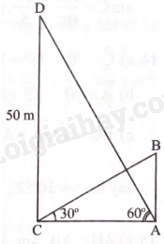
Ta có chiều cao của toà nhà và tháp lần lượt là AB, CD (đơn vị: m, AB > 0). Khi đó \(\widehat {ACB} = {30^o},\widehat {CAD} = {60^o}.\)
Xét tam giác ACD vuông tại C, ta có:
AC = DC.cot \(\widehat {CAD}\) = 50. cot 60o = \(\frac{{50\sqrt 3 }}{3}(m)\).
Xét tam giác ABC vuông tại A, ta có:
AB = AC. tan \(\widehat {ACB} = \frac{{50\sqrt 3 }}{3}.\tan {30^o} = \frac{{50}}{3} \approx 16,67(m).\)
Vậy toà nhà cao khoảng 16,67 m.
