Giải bài 5 trang 112 vở thực hành Toán 9 tập 2

Đề bài

Bạn Lan muốn cắt hình ngôi sao có dạng như hình dưới đây (trong đó ABCDE là một ngũ giác đều). Lan gấp đôi tờ giấy, vẽ một nửa ngôi sao và cắt theo nét vẽ. Góc tạo bởi lưỡi kéo và nếp gấp lúc đầu bằng bao nhiêu độ?

Phương pháp giải - Xem chi tiết

+ Ngũ giác đều ABCDE nội tiếp một đường tròn (O) và năm điểm A, B, C, D, E chia đường tròn (O) thành 5 cung nhỏ có số đo bằng \(\frac{{{{360}^o}}}{5} = {72^o}\).

+ Mỗi góc của ngũ giác đều là góc nội tiếp chắn cung bằng tổng của 3 cung nhỏ nên mỗi góc của ngũ giác đều bằng \(\frac{{{{3.72}^o}}}{2} = {108^o}\).

+ Gọi S là đỉnh trên cùng của ngôi sao.

+ Tính được \(\widehat {SAB} = {180^o} - \widehat {EAB}\), \(\widehat {SBA} = {72^o}\)\(\widehat {ASB} = {180^o} - \widehat {SAB} - \widehat {SBA}\).

+ Vì nếp gấp là trục đối xứng của ngôi sao nên sẽ nằm trên đường phân giác của góc ASB nên tính được góc tạo bởi lưỡi kéo và nếp gấp lúc đầu.

Lời giải chi tiết

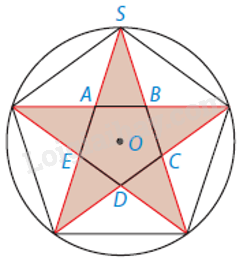
Ngũ giác đều ABCDE nội tiếp một đường tròn (O) và năm điểm A, B, C, D, E chia đường tròn (O) thành 5 cung nhỏ có số đo bằng \(\frac{{{{360}^o}}}{5} = {72^o}\). Mỗi góc của ngũ giác đều là góc nội tiếp chắn cung bằng tổng của 3 cung nhỏ nên mỗi góc của ngũ giác đều bằng \(\frac{{{{3.72}^o}}}{2} = {108^o}\).

Kí hiệu S là đỉnh trên cùng của ngôi sao. Khi đó, \(\widehat {SAB} = {180^o} - \widehat {EAB} = {72^o}\). Tương tự \(\widehat {SBA} = {72^o}\). Nên \(\widehat {ASB} = {180^o} - \widehat {SAB} - \widehat {SBA} = {36^o}\).

Vì nếp gấp là trục đối xứng của ngôi sao lên sẽ nằm trên đường phân giác của góc ASB. Do đó góc tạo bởi lưỡi kéo và nếp gấp phải bằng \(\frac{1}{2}{.36^o} = {18^o}\).

Bài trước Bài sau