Giải bài 5 trang 87 vở thực hành Toán 9

Đề bài

Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước. Biết rằng các khoảng cách từ một điểm C đến A và đến B là \(CA = 90m,CB = 150m\) và \(\widehat {ACB} = {120^o}\) (H.4.28). Hãy tính AB giúp bạn.

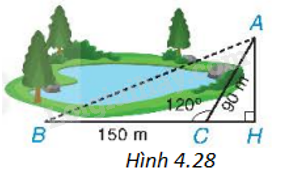
Phương pháp giải - Xem chi tiết

+ Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H.

+ \(\widehat {ACH} = {180^o} - \widehat {ACB} = {60^o}\)

+ Trong tam giác ACH vuông tại H nên \(HC = AC.\cos \widehat {ACH}\), tính được HC, \(AH = AC.\sin \widehat {ACH}\) tính được AH.

+ \(BH = BC + CH\)

+ Áp dụng định lí Pythagore vào tam giác ABH vuông tại H, tính được AB.

Lời giải chi tiết

Kẻ đường cao AH của tam giác ABC thì C nằm giữa B và H.

Trong tam giác ACH, ta có \(\widehat {ACH} = {180^o} - \widehat {ACB} = {60^o}\),

\(HC = AC.\cos \widehat {ACH} = 90.\cos {60^o} = 45\left( m \right)\)

\(AH = AC.\sin \widehat {ACH} = 90.\sin {60^o} = 45\sqrt 3 \left( m \right)\)

Từ đó, \(BH = BC + CH = 150 + 45 = 195\left( m \right)\)

\(A{B^2} = B{H^2} + A{H^2} = {195^2} + {\left( {45\sqrt 3 } \right)^2}\) suy ra \(AB = 210\left( m \right)\)

Bài trước Bài sau