-
SBT TOÁN TẬP 1 - CÁNH DIỀU
-
SBT TOÁN TẬP 2 - CÁNH DIỀU
Giải bài 50 trang 27 sách bài tập toán 12 - Cánh diều
Đề bài
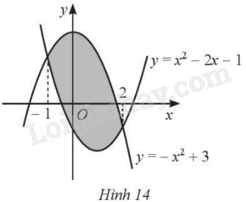
Cho hình phẳng được tô màu như Hình 14.
a) Hình phẳng đó được giới hạn bởi các đường nào?
b) Tính diện tích hình phẳng đó.
Phương pháp giải - Xem chi tiết
Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).
Lời giải chi tiết
a) Hình phẳng đã cho được giới hạn bởi đồ thị các hàm số \(y = {x^2} - 2{\rm{x}} - 1,y = - {x^2} + 3\) và hai đường thẳng \(x = - 1,x = 2\).
b) Diện tích hình phẳng được tính theo công thức:
\(\begin{array}{l}S = \int\limits_{ - 1}^2 {\left| {\left( {{x^2} - 2{\rm{x}} - 1} \right) - \left( { - {x^2} + 3} \right)} \right|dx} = \int\limits_{ - 1}^2 {\left[ {\left( { - {x^2} + 3} \right) - \left( {{x^2} - 2{\rm{x}} - 1} \right)} \right]dx} = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \\ = \left. {\left[ { - \frac{{2{{\rm{x}}^3}}}{3} + {x^2} + 4{\rm{x}}} \right]} \right|_{ - 1}^2 = \frac{{20}}{3} - \left( { - \frac{7}{3}} \right) = 9\end{array}\)