Giải bài 7.20 trang 34 sách bài tập toán 11 - Kết nối tri thức với cuộc sống

Đề bài

Cho tứ diện \(ABCD\) có \(AC = BC,AD = BD\). Gọi \(M\) là trung điểm của \(AB\). Chứng minh rằng \(\left( {CDM} \right) \bot \left( {ABC} \right)\) và \(\left( {CDM} \right) \bot \left( {ABD} \right)\).

Phương pháp giải - Xem chi tiết

Để chứng minh hai mặt phẳng \(\left( \alpha \right)\) và \(\left( \beta \right)\) vuông góc với nhau ta có thể dùng một trong các cách sau:

Chứng minh trong mặt phẳng này có một đường thẳng vuông góc với mặt phẳng kia. \(\left\{ \begin{array}{l}a \subset \left( \alpha \right)\\a \bot \left( \beta \right)\end{array} \right. \Rightarrow \left( \alpha \right) \bot \left( \beta \right)\).

+ Áp dụng tính chất trung tuyến của tam giác cân

Lời giải chi tiết

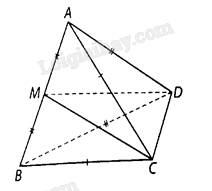
Vì \(M\) là trung điểm của \(AB\) nên \(AB \bot CM\), \(AB \bot DM\), suy ra \(AB \bot \left( {CDM} \right)\).

Vì hai mặt phẳng \(\left( {ABC} \right)\) và \(\left( {ABD} \right)\) đều chứa đường thẳng \(AB\) nên \(\left( {ABC} \right) \bot \left( {CDM} \right),\left( {ABD} \right) \bot \left( {CDM} \right)\).

Bài trước Bài sau