Giải bài 8 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 1

Đề bài

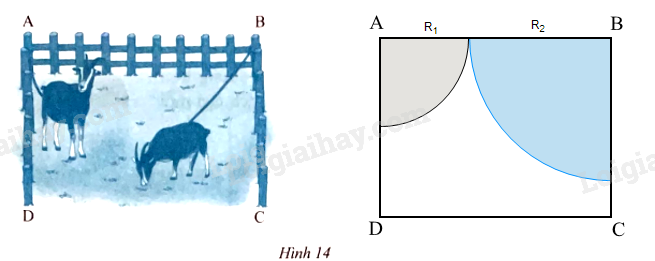
Một vườn cỏ có dạng hình chữ nhật ABCD với AB = 40 m, AD = 30 m. Người ta muốn buộc hai con dê ở hai góc vườn A, B. Có hai cách buộc:

Cách 1: Mỗi dây thừng dài 20 m.

Cách 2: Một dây thừng dài 30 m và một dây thừng dài 10 m.

Hỏi với cách buộc nào thì diện tích cỏ mà hai con dê có thể ăn được sẽ lớn hơn?

 

Lời giải chi tiết

Diện tích cỏ hai con dê có thể ăn là dạng hai hình quạt có số đo cung cùng bằng 90^o.

TH1: Mỗi dây thừng dài 20 m suy ra R₁ = R₂ = 20 m.

Diện tích cỏ mà hai con dê có thể ăn:

\(S = {S_1} + {S_2} = \frac{{\pi R_1^2.90}}{{360}} + \frac{{\pi R_2^2.90}}{{360}} \\= \frac{{\pi {{.20}^2}.90}}{{360}} + \frac{{\pi {{.20}^2}.90}}{{360}} = 200\pi ({m^2})\)

TH2: Giả sử dây thừng cột con dê ở A dài 30 m, dây thừng cột con dê ở B dài 10 m.

Suy ra R₁ = 30 m, R₂ = 10 m.

Diện tích cỏ mà hai con dê có thể ăn:

\(S = {S_1} + {S_2} = \frac{{\pi R_1^2.90}}{{360}} + \frac{{\pi R_2^2.90}}{{360}} \\= \frac{{\pi {{.30}^2}.90}}{{360}} + \frac{{\pi {{.10}^2}.90}}{{360}} = 250\pi ({m^2}).\)

Vậy dùng hai sợi dây 30 m và 10 m thì diện tích cỏ hai con dê sẽ ăn nhiều hơn.